Окружность, вписанная в треугольник авс касается стороны вс в точке к. докажите что ск=p-ав где р полупериметр треугольника авс

))) Интересное задание, сначала не хотел браться, потом "зацепило"...

Смотрим рисунок и вспоминаем свойство касательных:

Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности (вот почему, собственно, центр вписанной в треугольник окружности лежит в точке пересечения биссектрис...).

Пусть точки М, К и О - точки касания окружности со сторонами АВ, ВС и АС, соответственно.

Из свойства касательных следует, что:

Периметр (пока в рассчётах берём именно периметр Р (большая), а не полупериметр р (малая)):

, значит

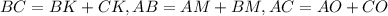Так как , то:

Исходя из вышеприведённых равенств:

Имеем право записать как:

В нижней записи у нас уже фигурирует полупериметр р (малая). ЧТД

Как "Лучшее решение" не забудь отметить, ОК?!.. ;)))