Окружность с диаметром AB, где A(0; -2), B(8; 4), задается уравнением (обязательно с решением): 1) 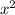 +
+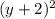 =16
=16
2) 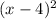 +
+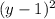 =25
=25
3) 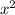 +
+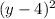 =16
=16
4) 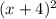 +
+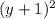 =25
=25
Другие вопросы по теме Геометрия
Популярные вопросы
- Функція g є такою, що g(-6)=5. Тоді g(6)*g(-6)=, якщо функція парна,...
2 - Записать в тетради список расширений файлов. К заданию прикрепить...
3 - 144. Сравни метро и троллейбус, автобус и трамвай. В чем их сходство...
1 - Переведите 6 400 м^2/c^2 в м/c...
1 - Дан угол α = 45°, который луч OA образует с положительной полуосью...
1 - ЖАЗЫЛЫМ АЙТЫЛЫМ -тапсырма. Соңғы жылдары Қазақстанда қандай фильмдер...
2 - Заполните таблицу «Классицизм и сентиментализм», опираясь на материалы...
3 - сочинение 6 класс «Почему Дубровский стал разбойником?» ПО ПЛАНУ!...
1 - Выполни задания после текста Две женщины брали воду из колодца. Подошла...
1 - Шар массой 185 г сталкивается со вторым шаром неизвестной массы. Ускорения,...
3
Давай начнем с первого уравнения:
1) x^2 + (y+2)^2 = 16
Уравнение окружности выглядит следующим образом: (x-a)^2 + (y-b)^2 = r^2, где (a, b) - координаты центра окружности, r - радиус окружности.
В данном уравнении, центр окружности можно найти, заметив, что коэффициенты x и y равны 0, а радиус равен 4. Так что центр окружности будет иметь координаты (0, -2), а радиус будет равен 4.
Теперь перейдем ко второму уравнению:
2) (x-4)^2 + (y-1)^2 = 25
Аналогично, заметим что коэффициенты x и y равны 4 и 1 соответственно, а радиус равен 5. Значит, центр окружности будет иметь координаты (4, 1), а радиус будет равен 5.
Перейдем к третьему уравнению:
3) x^2 + (y-4)^2 = 16
Здесь у нас коэффициенты x и y равны 0 и 4 соответственно, а радиус снова будет равен 4. Так что центр окружности будет иметь координаты (0, 4), радиус окружности - 4.
И, наконец, четвертое уравнение:
4) (x+4)^2 + (y+1)^2 = 25
Коэффициенты x и y равны -4 и -1 соответственно, а радиус равен 5. Центр окружности будет иметь координаты (-4, -1), а радиус - 5.
Таким образом, мы нашли центры и радиусы каждой окружности. Надеюсь, это поможет тебе в дальнейшем изучении геометрии. Если у тебя возникнут еще вопросы, не стесняйся обратиться ко мне. Удачи!