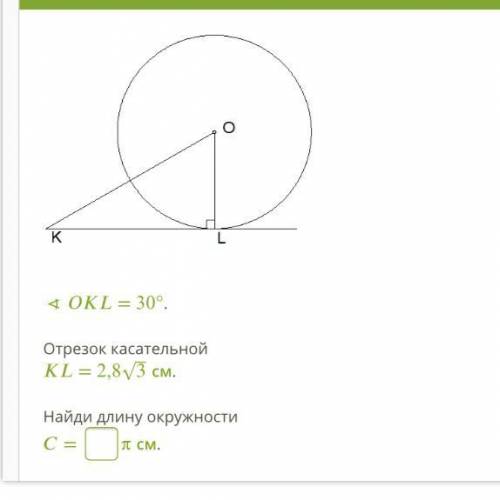
OKL= 30°. Отрезок касательной
KL= 2,83‾√ см.

Найди длину окружности
C= п см.

(Если необходимо, ответ округли до сотых)

Для решения данной задачи, нам нужно знать некоторые основные свойства окружностей.

Длина окружности выражается формулой C = 2 * π * r, где C - длина окружности, r - радиус окружности, π (пи) - математическая постоянная, примерное значение которой равно 3,14159.

В данной задаче у нас известны длина отрезка KL и угол OKL. Мы можем воспользоваться свойствами треугольников, вписанных в окружность, чтобы найти радиус и, следовательно, длину окружности.

Сначала нам нужно найти длину отрезка KO, а затем длину отрезка OL.

Так как у нас есть прямоугольный треугольник OKL и угол OKL равен 30 градусам, мы можем воспользоваться соотношениями тригонометрии.

В прямоугольном треугольнике OKL, где угол OKL равен 30 градусам, мы знаем, что тангенс угла равен отношению противолежащего катета к прилежащему.

Тангенс угла OKL = KL / KO.

Так как нам дана длина отрезка KL, а значит тангенс угла, мы можем найти длину отрезка KO:

KO = KL / тангенс угла OKL.

Так как KL = 2,83‾√ см и угол OKL = 30 градусов, мы можем найти тангенс угла OKL, подставив значения и упростив выражение:

тангенс 30 градусов = 1 / √3.

Теперь мы можем найти длину отрезка KO:

KO = 2,83‾√ / (1 / √3).

Для упрощения выражения нам нужно запомнить, что деление на дробь эквивалентно умножению на обратную дробь:

KO = 2,83‾√ * √3.

KO = 2,83 * √3.

Теперь мы можем найти длину отрезка OL, используя те же самые шаги. В данном случае, тангенс угла OLL' = 1 / √3 и OL = KL:

OL = KL / тангенс угла OLL'.

Таким образом:

OL = 2,83‾√ / (1 / √3).

OL = 2,83‾√ * √3.

OL = 2,83 * √3.

Мы нашли длины отрезков KO и OL, теперь нам нужно найти радиус окружности относительно этих отрезков.

Радиус окружности равен половине диаметра, а диаметр равен сумме длин отрезков KO и OL:

r = (KO + OL) / 2.

r = (2,83 * √3 + 2,83 * √3) / 2.

r = (2 * 2,83 * √3) / 2.

r = 2,83 * √3.

Таким образом, мы нашли радиус окружности. Теперь мы можем найти длину окружности, используя формулу C = 2 * π * r:

C = 2 * π * r.

C = 2 * 3,14159 * (2,83 * √3).

C = 2 * 3,14159 * 2,83 * √3.

C = 17,766475 * √3.

Ответ: Длина окружности (C) примерно равна 17,77 * √3 см. (запишите см, так как это единица измерения длины).

Надеюсь, это решение понятно для школьников и помогает вам выполнить задачу. Если у вас возникнут еще вопросы, не стесняйтесь задавать.