1. Геометрия
  2. Одна із сторін трикутника

Одна із сторін трикутника дорівнює 2 а прилеглі до неї кути дорівнюють 30 град і 45 град. знайти площу трикутника подробно )) ответ 0,73 приблизительно

Pechenka100500 Pechenka100500    3   03.09.2019 13:10    13

Ответы
zaurezhunus zaurezhunus  06.10.2020 14:48
ΔАВС , АВ=2 , ∠А=30° , ∠В=45°

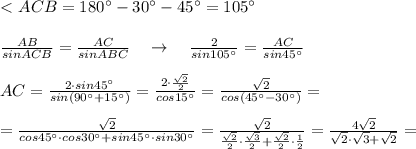
\\\\ \textless \ ACB=180^\circ-30^\circ-45^\circ=105^\circ \\\\\frac{AB}{sinACB}=\frac{AC}{sinABC} \quad \to \quad \frac{2}{sin105^\circ }=\frac{AC}{sin45^\circ }\\\\AC= \frac{2\cdot sin45^\circ }{sin(90^\circ +15^\circ )}= \frac{2\cdot \frac{\sqrt2}{2}}{cos15^\circ}= \frac{\sqrt2}{cos(45^\circ-30^\circ)} =\\\\=\frac{\sqrt2}{cos45^\circ \cdot cos30^\circ +sin45^\circ \cdot sin30^\circ }= \frac{\sqrt2}{\frac{\sqrt2}{2}\cdot \frac{\sqrt3}{2}+\frac{\sqrt2}{2}\cdot \frac{1}{2}}= \frac{4\sqrt2}{\sqrt2\cdot \sqrt3+\sqrt2}=

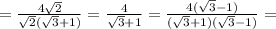
=\frac{4\sqrt2}{\sqrt2(\sqrt3+1)}=\frac{4}{\sqrt3+1}= \frac{4(\sqrt3-1)}{(\sqrt3+1)(\sqrt3-1)}=

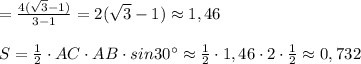
=\frac{4(\sqrt3-1)}{3-1} = 2(\sqrt3-1)\approx 1,46\\\\S=\frac{1}{2}\cdot AC\cdot AB\cdot sin30^\circ \approx \frac{1}{2}\cdot 1,46\cdot 2\cdot \frac{1}{2}\approx 0,732
ПОКАЗАТЬ ОТВЕТЫ
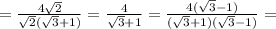
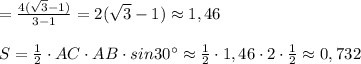
Другие вопросы по теме Геометрия
АнастасияКот26 АнастасияКот26  16.12.2020 16:31
Знайти площу основи конуса, якщо радіус дорівнює 2м...
akovlevavika444 akovlevavika444  16.12.2020 16:30
Найдите катет если гипотенуза равна 6см а второй катет равен 5см (ЧЕРТЕЖ)...
arsjaja arsjaja  16.12.2020 16:30
На рисунке изображен прямоугольник АВСD, на сторонах которого внутри него построены равные равнобедренные треугольники:  АВМ = CDP, BCN = ADG. Докажите, что четырехугольник MNPG –...
iratsymbal7 iratsymbal7  16.12.2020 16:30
добрые люди только d e​ побыстрее не знаете не заходите...
Koshaplay57 Koshaplay57  21.05.2019 05:00
С, ! 1. в трапецию, основания которой 3 см и 5 см, вписана окружность радиуса 2 см. найдите площадь и периметр трапеции. 2. сторона треугольника 60 см, 61 см, 11...
Dk2205 Dk2205  21.05.2019 05:00
Втреугольнике abc угол c равен 88, ad и be- биссектрисы, пересекающиеся в точке о.найдите угол aob....
Наташа12Няша Наташа12Няша  21.05.2019 05:00
Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в 1,5 раза?...
ElzaMi13 ElzaMi13  21.05.2019 05:00
Втреугольнике авс угол в равен 56 градусов, угол с равен 64 градуса, вс=3 корней из 3. найдите радиус описанной около этого треугольника окружности....
маринчик18 маринчик18  20.11.2020 09:32
Извините за качество.решити...
Svetlana2675 Svetlana2675  20.11.2020 09:32
Признаки равенства треугольников (2-й признак)Определи по рисунку равные треугольники:​...

Популярные вопросы