1. Геометрия
  2. Одна из сторон треугольника

Одна из сторон треугольника равна ✓6, а прилегающие к ней углы - 60° и 75°. найдите вторую сторону треугольника, которая прилегает к углу 75°

knoposhka123 knoposhka123    3   02.02.2020 23:39    6

Ответы
полина2054 полина2054  11.10.2020 04:04

Сторона = 3

Объяснение:

Построим ΔABC, где BC =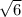 \sqrt{6}, ∠B = 60°, ∠C = 75°

∠A = 180° - 60° - 75° = 45°

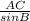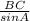
По теореме синусов - \frac{AC}{sinB} = \frac{BC}{sinA}

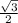
sin∠B = \frac{\sqrt{3} }{2}

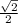
sin∠A = \frac{\sqrt{2} }{2}

\frac{AC * 2}{\sqrt{3} } = \frac{\sqrt{6} * 2 }{\sqrt{2} }

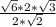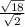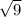AC = \frac{\sqrt{6} * 2 * \sqrt{3} }{2 * \sqrt{2} } = \frac{\sqrt{18} }{\sqrt{2} } = \sqrt{9} = 3

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
VictoriaOrlova32455 VictoriaOrlova32455  06.10.2019 06:30
Вариант 2 1. отрезки ав и см пересекаются в точке о так. что ас | вм. найдите длину отрезка см, если ас=15 см, вм 3 см, со =10 см. 2. высота прямоугольного треугольника, проведенная...
61551 61551  06.10.2019 06:30
1. построить две прямые, пересеченные третьей. отметить и подписать на чертеже одностороние, накрест лежащие, соответственные, вертикальные и смежные углы. 2.записать определение...
bbb87 bbb87  06.10.2019 06:30
Haйдитe рaсстoяние oт тoчки m дo плоскости равностороннего треугольника если сторона этого треугольника равна 3√3 см а расстояние от точки м до каждой из вершин треугольника равно...
blecstar2000 blecstar2000  06.10.2019 06:30
Биссектриса равностороннего треугольника равна 12 см .чему равен радиус окружности, описанной около этого треугольника. нужно...
Xaby Xaby  10.07.2021 12:15
развертка боковой поверхности конуса представляет собой четверть круга радиуса 4/корень из пи. Найдите площадь полной поверхности конуса...
GreenExtreme5995 GreenExtreme5995  10.07.2021 12:14
в треугольнике ABC на стороне BC взята точка M, а на стороне BC- точка N, так, что AM:MB=1:3, BN:NC = 1:1. Отрезки AN и CM пересекаются в точке o, найдите площадь CON, если площадь...
попаоп попаоп  10.07.2021 12:05
знайди площу трикутного схилу залізного даху якщо основа цього трикутника a=b,5м а його висота h=5,25м...
ввіна ввіна  10.07.2021 12:03
Площа S=0,06га Основа 40м Обчислити висоту...
zvezdoska zvezdoska  10.07.2021 11:22
Найдите высоту самого большого объемного цилиндра, нарисованного внутри полусферы площадью 27п.​...
olenkayatsev olenkayatsev  10.07.2021 11:16
какое наименьшее число прямоугольников с изменениями 8 и 20 надо взять, что бы из них можно было бы сложить квадрат объяснить ответ​...

Популярные вопросы