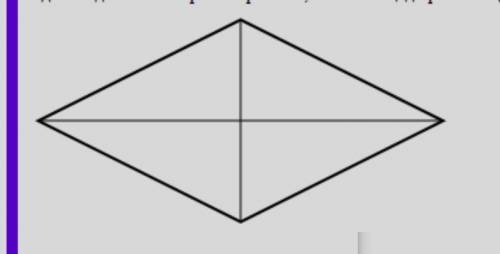
Одна из диагоналей ромба равна 2, а его площадь равна 2 √3. найдите сторону ромба

Ответы

smolyarrrovav 28.11.2021 16:50

Пусть извесная диагональ - это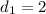 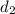d_1=2 , d_2 - неизвестная диагональ, а 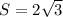$S=2\sqrt{3}$ - площадь ромба.

По формуле площади ромба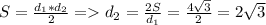 $S=\frac{d_1*d_2}{2} =d_2=\frac{2S}{d_1} =\frac{4\sqrt{3} }{2}=2\sqrt{3}$ .

Ромб разделен диагоналями на четыре прямоугольных треугольника, катетами которых равняются половины диагоналей, а гипотенузой - сторона ромба.

Поэтому, используя теорему Пифагора имеем, что сторона ромба равна: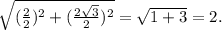 $\sqrt{(\frac{2}{2})^2+(\frac{2\sqrt{3} }{2})^2} =\sqrt{1+3}=2.$

ОТВЕТ: 2.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

Багирая 25.09.2019 23:10

Накопитель тепла и основной источник влаги...

VaBaGaBa 25.09.2019 21:59

ariannaajoseph9 25.09.2019 23:10

mru199 25.09.2019 21:59

80 і 76,78,80. або рішіть який зможете будьласка)...

anastasia1231234 25.09.2019 23:10

Ivangggg 25.09.2019 21:58

1)в прямоугольнике abcd сторона ab=10,...

Nastya250420021 25.09.2019 23:10

Zacloock 25.09.2019 21:56

danya166 19.08.2019 22:30

Дано: δabc a=c ab: ac=13: 11 ab-ac=2,1см найти ab,bc,ac...

adelinathebest 19.08.2019 22:30