Одна из диагоналей ромба на 8 см больше другой , а его площадь равна 384 кв.см . найти сторону ромба .

Объяснение:площадь ромба равна произведение диагоналей делённое на 2. Обазначим одну диагональ за х, тогда вторая диагональ х+8. Составляем уравнение.

384=х(х+8)/2

76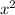8=+8

Находим дискриминант. D=64+3072=3136

х1=-8+56/2=24

х2=-8-56/2=-32

значит первая диагональ равна 24 см,а вторая 32 см.

Теперь мы помним что диагонали точкой пересечения делятся пополам. Значит мы имеем треугольник в котором катеты половины от диагоналей, а гипотенуза это сторона ромба. По теореме пифагора:

144+256=400

Значит сторона ромба равна: 20 СМ