Один із катетів прямокутного трикутника дорівнює 30 см,а радіус описаного навколо нього кола -17 см.обчисліть площу даного трикутника

Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы. Т.к. R=17 см, то гипотенуза = 34 см. По т. Пифагора второй катет равен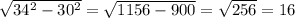 см

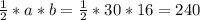S= см^2

Один из катетов прямоугольного треугольника равен 30 см, а радиус описанной вокруг него окружности - 17 см. Вычислить площадь данного треугольника.

Гипотенуза треугольника является диаметром описанной окружности.

Второй катет b = √34²-30²=√256=16 cм

Площадь тр-ка S = a*b/2 = 30*16/2 = 240см²