Один угол треугольника в 2 раза меньше другого, а противоположные от них стороны равны 5 и 8. Найдите
радиус окружности, описанной вокруг треугольника.

Один угол треугольника в 2 раза меньше другого, а

противоположные от них стороны равны 5 и 8. Найдите

радиус окружности, описанной вокруг треугольника.

Объяснение:

Пусть меньший угол α-против этого угла лежит сторона  5,

тогда больший угол 2α-против этого угла лежит  сторона 8.

По т. синусов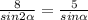  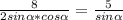    , , cosα=0,8 .

По основному тригонометрическому тождеству sinα=√(1-0,8²)=0,6 .

По т. синусов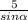    =2R , 2R*0,6=5  ,R=  .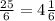