Один из острых углов прямоугольного треугольника равен 60° . из этого угла выходит биссектриса равна 8 см. найти катет напротив этого угла.

Ответы

lena08m 06.10.2020 01:28

Углы, на которые разбивает биссектриса угол в 60°, равны по 30°.

На рисунке я обозначил c - гипотенуза, a - прилежащий к углу 60° катет,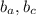 b_a,b_c - отрезки, на которые биссектриса делит катет b.

$$cos60^\circ=\boxed{\frac{a}{c}= \frac{1}{2}}$

Далее, по свойству биссектрисы имеем

$$\frac{a}{b_a}=\frac{c}{b_c} \Rightarrow \frac{a}{c}=\boxed{\frac{b_a}{b_c}=\frac{1}{2}}$ (1/2 из предыдущего вывода)

Далее, рассмотрим прямоугольный треугольник с биссектрисой в качестве гипотенузы и запишем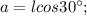 $a=lcos30^{\circ};$

По теореме Пифагора в нем же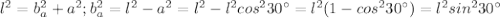 $l^2=b^2_a+a^2; b_a^2=l^2-a^2=l^2-l^2cos^230^{\circ}=l^2(1-cos^230^{\circ})=l^2sin^230^{\circ}$

То есть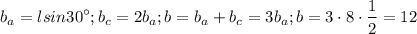 $$b_a=lsin30^{\circ}; b_c=2b_a; b=b_a+b_c=3b_a; b=3\cdot8 \cdot\frac{1}{2} =12$

ответ: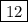 $\boxed{12}$

ПОКАЗАТЬ ОТВЕТЫ

rzhanova00 06.10.2020 01:28

$4\sqrt{3}$ cм

Объяснение:

По формуле биссектриса равна:

$L = a\sqrt{\frac{2}{1+cos\beta}}$ , где а - катет, L - биссектриса, а β наш угол в 60°.

Подставим сюда наши значения:

$8 = a\sqrt{\frac{2}{1+cos60}} = a\sqrt{\frac{2}{1+\frac{1}{2}}} = a\sqrt{\frac{2}{\frac{3}{2}}} = a\sqrt{\frac{2*2}{3}} = a\frac{\sqrt{4}}{\sqrt{3}} = \frac{2a}{\sqrt{3}} = a\frac{2\sqrt{3}}{3}$

$a = \frac{8}{\frac{2\sqrt{3}}{3}} = \frac{8*3}{2\sqrt{3}} = \frac{4*3}{\sqrt{3}} = \frac{12}{\sqrt{3}} = \frac{12\sqrt{3}}{3} = 4\sqrt{3}$ .

Удачи!

Один из острых углов прямоугольного треугольника равен 60° . из этого угла выходит биссектриса равна

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

Aleksandra231v 13.05.2020 11:25

Решите задачу по геометрии плес...

elen19871 13.05.2020 11:25

Найдите гипотенузу. Если несложно, ещё остальные два задания....

настя7500 13.05.2020 11:25

Трикутник ABC рівнобедрений з основою BC . укажіть неправильне твердження а)сторони ABі ACрівні в)медіана AMперпердекулярна до BC б)кути ABC і ACB рівні г) висота ВК є бісектрисою...

kokosik23 13.05.2020 11:25

Бессиктрисы АК и БМ треугольника ABC пересекаются в точке O. Найдите угол C треугольника , если угол KOB=70градусов...

Shishmariya 13.05.2020 11:25

Одна з сторін дорівнює 8 см, а прилеглі до неї кути 60 і 45 . Знайдіть висоту, проведену до цієї сторони....

Venjin 13.05.2020 11:25

Найти x и y (не только ответ а решение тоже с объяснениеми)...

daviduk2509 13.05.2020 11:25

У рівнобедреному трикутнику АВК з основою АК проведено медіани АМ і КЕ. Довести що кут АЕК = куту КМА....

Артём244 13.05.2020 11:25

В трапеции ABCDABCD (AD∥BCAD∥BC) ∠ABC=96∘∠ABC=96∘ и ∠ADC=48∘∠ADC=48∘. На луче BABA за точкой AA отметили точку KK такую, что AK=BCAK=BC. Найдите угол DKCDKC, если известно, что ∠BKC=24∘∠BKC=24∘....

Garik23123 21.12.2020 15:41

Площа осьового перерізу циліндра 12 см2 а висота циліндра 4 см. Знайти діаметр циліндра...

vikaivanyk 30.06.2019 01:40

Известен периметр равнобедренного треугольника 50 см основание в два раза меньше стороны надо найти все стороны : решение ?...

Один из острых углов прямоугольного треугольника равен 60° . из этого угла выходит биссектриса равна 8 см. найти катет напротив этого угла.

Популярные вопросы