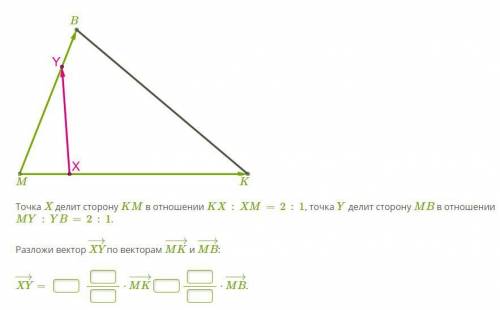
ОЧЕНЬ Точка X делит сторону KM в отношении KX:XM=2:1, точка Y делит сторону MB в отношении MY:YB=2:1.
Разложи вектор XY−→ по векторам MK−→− и MB−→−:
XY−→=
⋅MK−→−
⋅MB−→−.
мне влепят 2 если не решу. а потом это скажется на годовой и четверти и не пустят на работу и буду бомжевать ._.
Другие вопросы по теме Геометрия
Популярные вопросы
- Сөздерден біріктер сөзді белгіле А.Музыка В.Күйші С. Таршылық Д.шанқобыз...
3 - Напишите следующие математические выражения на языке программирования...
2 - Какой заряд проходит по каналу молнии за время разряда 3 мс при силе...
3 - Как соотносятся понятия: миоцит, мышечное волокно, гладкая мышца,...
1 - текст на фото зделаю лутшим ответом...
2 - На сторонах угла ∡ ABC точки A и C находятся на равных расстояниях...
2 - БЫСТРЕЕ Опишите схему1 и схему2 подключения оборудования. Схема1...
2 - Задание в вопросе. Не понимаю как делать проекцию во втором случае...
1 - 3 сынып 52 бет 23 жаттыгу 2 болим комектесиндпрши отинем!...
2 - Шұнтиып қос құлағы Түнде көрер қырағы.Тікірейіп айдары,Егін жауын...
3
1. Начнем с того, что нам дано. У нас есть треугольник KMB, в котором точка X делит сторону KM в отношении KX:XM=2:1, а точка Y делит сторону MB в отношении MY:YB=2:1.
2. Теперь нам нужно найти вектор XY−→ по векторам MK−→− и MB−→−. Для этого возьмем вектор MK−→− и умножим его на коэффициент пропорциональности KX:XM.
Вектор MK−→− это направленный отрезок, соединяющий точку M с точкой K. Мы не знаем конечные координаты точек M и K, поэтому мы не можем найти конкретное численное значение вектора MK−→−.
Однако, мы можем записать вектор MK−→− в общей форме, используя координаты точек M и K. Пусть координаты M равны (x1, y1), а координаты K равны (x2, y2). Тогда вектор MK−→− будет иметь вид: MK−→− = (x2 - x1, y2 - y1).
3. Теперь мы должны умножить вектор MK−→− на коэффициент пропорциональности KX:XM. У нас дано, что KX:XM=2:1, поэтому мы можем записать этот коэффициент в виде 2/1. Умножим каждую компоненту вектора MK−→− на этот коэффициент:
KX−→=(2/1)(x2 - x1, y2 - y1)= (2*(x2 - x1), 2*(y2 - y1)).
4. Теперь мы должны разложить вектор XY−→ по векторам MK−→− и MB−→−. Это означает, что мы должны представить вектор XY−→ в виде суммы этих векторов.
Разложим вектор XY−→ по вектору MK−→−:
XY−→= MK−→− + KX−→ = (x2 - x1, y2 - y1) + (2*(x2 - x1), 2*(y2 - y1)).
5. Наконец, разложим вектор XY−→ по вектору MB−→−. Вектор MB−→− это направленный отрезок, соединяющий точку M с точкой B. Аналогично шагу 2, запишем вектор MB−→− в общей форме, используя координаты точек M и B. Пусть координаты B равны (x3, y3). Тогда вектор MB−→− будет иметь вид: MB−→− = (x3 - x1, y3 - y1).
Разложим вектор XY−→ по вектору MB−→−:
XY−→= XY−→ - KX−→ - MK−→− = (x2 - x1, y2 - y1) + (2*(x2 - x1), 2*(y2 - y1)) - (x3 - x1, y3 - y1).
Таким образом, мы разложили вектор XY−→ по векторам MK−→− и MB−→−. Надеюсь, что это решение помогло вам понять данную задачу. Если у вас остались еще вопросы, пожалуйста, не стесняйтесь задавать их. Удачи!