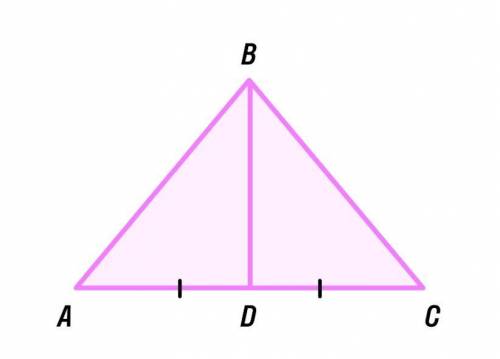
Очень ! Простите, много обещать не могу :( В треугольнике ABC медиана BD делит угол ABC пополам. Найди сторону AB этого треугольника, если BD = 5, tg угла ACB = 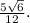
Другие вопросы по теме Геометрия
Популярные вопросы
- Вычислить площадь фигуры, ограниченной линиями у = , у = х2 + 3, х =...
3 - S Now imagine you are in the volleyball mit your answer to the intenquestionssly...
3 - Знайти кути при основі рівнобедреного трикутника бічними сторонами є...
1 - завтра уже надо сдавать а я тему не понял 643,644,646 номер умоляю аоаооаоаоаоаоаоаоаоаоаао...
3 - Твір на тему :Чого може навчитися сучасний школяр у героїв Жуля Верна....
2 - Хелп , 16 во второй степени умножить на 3 / 12 в степени 4 . ...
3 - Види дiяльностi русичiв. быстрее...
2 - Выборочное изложение 5 класс упр 269...
3 - 8. Прачытайце ўрывак з верша Петруся Броўкі «Дарагая Беларусь».Не магло...
1 - При яких значеннях параметра а рівняння нижче має корені різного знаку?...
1
1. Воспользуемся теоремой о медиане в треугольнике: медиана делит сторону, которую она пересекает, пополам. В данной задаче у нас медиана BD, поэтому сторона AD равна стороне DB.
2. Поскольку угол ABC делится медианой пополам, то угол ABD равен углу CBD. Пусть общая мера этих углов равна x. Тогда мера угла ABD равна x, а мера угла CBD также равна x.
3. Так как угол ABD равен углу CBD, то угол ADC является прямым углом (180 градусов).
4. Рассмотрим прямоугольный треугольник ADC. Мы знаем, что tg угла ACB равен \(\frac{5\sqrt6}{12}\). Возьмем соответствующие стороны треугольника ADC: противолежащую углу ACB (сторону AD) и прилежащую (сторону CD).
5. Используя теорему тангенсов, запишем: tg угла ACB = \(\frac{AD}{CD}\). Подставляем известные значения: \(\frac{5\sqrt6}{12} = \frac{AD}{CD}\).
6. Поскольку сторона AD равна стороне DB (по теореме о медиане), то AD = 5.
7. Подставляем полученное значение и продолжаем решение: \(\frac{5\sqrt6}{12} = \frac{5}{CD}\).
8. Решаем полученное уравнение относительно CD: \(CD = \frac{5}{\frac{5\sqrt6}{12}} = \frac{12}{\sqrt6} = \frac{12\sqrt6}{6} = 2\sqrt6\).
9. Теперь мы знаем значения двух сторон треугольника, AB и CD. Поскольку сторона AB равна сумме сторон AD и CD (по теореме о медиане), получаем: AB = AD + CD = 5 + 2\sqrt6.
10. Ответ: сторона AB треугольника ABC равна 5 + 2\sqrt6.
Надеюсь, это понятное и подробное решение помогло вам понять, как решать данную задачу. Если остались еще вопросы, с удовольствием помогу."