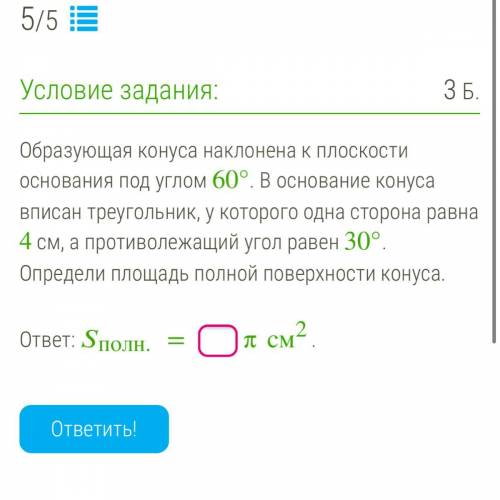
Образующая конуса наклонена к плоскости основания под углом 60°. В основание конуса вписан треугольник, у которого одна сторона равна 4 см, а противолежащий угол равен 30°. Определи площадь полной поверхности конуса.

Для решения данной задачи, нам необходимо определить площадь полной поверхности конуса.

Поскольку образующая конуса наклонена к плоскости основания под углом 60°, у нас есть правильный треугольник ABC, который является основанием конуса. При этом сторона треугольника AB равна 4 см, а противолежащий угол A равен 30°.

Нам также известно, что образующая конуса (показанная на рисунке как AC) образует угол 60° с плоскостью основания. Пусть точка D - нижний конец образующей конуса AC (с ключом или шляпкой).

Теперь давайте обратимся к рисунку, чтобы определить площадь сторон конуса.

Обозначим точку E как точку пересечения высоты BH и образующей AC.

Высота BH - это высота, опущенная из вершины конуса B на основание ABC, а точка M - середина стороны AC.

Поскольку ABC - правильный треугольник, высота BH является медианой и делит сторону AC пополам.

Таким образом, мы можем сказать, что EM = MC = 2 см.

Поскольку треугольник ABE состоит из прямого угла ABE (30°), прямого угла ABM (90°) и прямого угла BEM (90°), он является прямоугольным треугольником.

Мы можем использовать тригонометрию, чтобы определить длину стороны AE:

sin A = EM / AE
sin 30° = 2 / AE
1/2 = 2 / AE
AE = 4 см

Теперь мы можем определить высоту BH с использованием теоремы Пифагора в треугольнике ABH:

BH^2 = AB^2 - AH^2
BH^2 = 4^2 - 2^2
BH^2 = 16 - 4
BH^2 = 12
BH = √12 = 2√3 см

Таким образом, мы определили высоту BH равной 2√3 см.

Теперь давайте определим площади основания и боковой поверхности конуса:

Площадь основания конуса, которая равна площади треугольника ABC, можно определить с использованием формулы для правильного треугольника:

Площадь ABC = (AB^2 * √3) / 4
Площадь ABC = (4^2 * √3) / 4
Площадь ABC = 4√3 кв.см

Теперь давайте определим площадь боковой поверхности конуса.

Боковая поверхность конуса представляет собой поверхность, которая образуется при развертывании боковой поверхности конуса.

У нас есть правильный треугольник AED, в котором сторона AE равна 4 см, а высота ED равна 2√3 см. Мы можем определить площадь этого треугольника с использованием формулы для треугольника:

Площадь AED = (AE * ED) / 2
Площадь AED = (4 * 2√3) / 2
Площадь AED = 4√3 кв.см

Теперь, чтобы определить площадь боковой поверхности конуса, мы должны умножить площадь AED на число π (пи) и на радиус конуса AC (который равен длине стороны AE):

Площадь боковой поверхности конуса = Площадь AED * π * AC
Площадь боковой поверхности конуса = (4√3 кв.см) * π * 4 см
Площадь боковой поверхности конуса = 16√3π кв.см

Теперь мы можем найти площадь полной поверхности конуса, сложив площадь основания и площадь боковой поверхности:

Площадь полной поверхности конуса = Площадь основания + Площадь боковой поверхности конуса
Площадь полной поверхности конуса = 4√3 кв.см + 16√3π кв.см

Таким образом, площадь полной поверхности конуса составляет 4√3 кв.см + 16√3π кв.см.