1. Геометрия
  2. Нужно свериться с ответом: а1,

Нужно свериться с ответом: а1, а2, а3, а4 - вершины пирамиды. найдите угол между ребрами а1а2 и а1а4, проекцию вектора а1а3 на вектор а1а4, если а1 (4; 6; 5) а2 (6; 9; 4) а3 (2; 10; 10) а4(7; 5; 9)угол между а1а2 и а1а4 = 1/2sqrt(91)?

ksyxa92 ksyxa92    1   05.10.2019 17:40    0

Ответы
Maximismailov281 Maximismailov281  09.10.2020 22:07

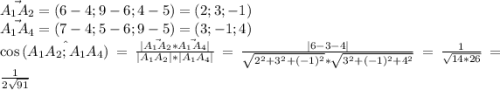
1) \vec{A_1A_2}=(6-4;9-6;4-5)=(2;3;-1)\\\vec{A_1A_4}=(7-4;5-6;9-5)=(3;-1;4)\\\cos{\hat{(A_1A_2;A_1A_4)}}=\frac{|\vec{A_1A_2}*\vec{A_1A_4}|}{|A_1A_2|*|A_1A_4|}=\frac{|6-3-4|}{\sqrt{2^2+3^2+(-1)^2}*\sqrt{3^2+(-1)^2+4^2}}=\frac{1}{\sqrt{14*26}}=\frac{1}{2\sqrt{91}}

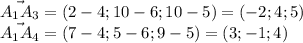
2) \vec{A_1A_3}=(2-4;10-6;10-5)=(-2;4;5)\\\vec{A_1A_4}=(7-4;5-6;9-5)=(3;-1;4)

Проекция вектора  a на направление вектора  b равна скалярному произведению этих векторов, деленному на длину вектора b:

Pr_{\vec{A_1A_4}}\vec{A_1A_3}=\frac{(\vec{A_1A_3},\vec{A_1A_4})}{|\vec{A_1A_4}|}=\frac{-6-4+20}{\sqrt{3^2+(-1)^2+4^2}}=\frac{10}{\sqrt{26}}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
KarakatitsaKrutitsa KarakatitsaKrutitsa  26.07.2019 08:10
Дано: треугольник авс,ад-биссектриса, уголауголс=121 град, угол авс=101 град. найти угол асв...
Elina1987 Elina1987  26.07.2019 08:10
Поверхность двух шаров относится как 25: 36. как относятся их объемы?...
Дллллллллллл Дллллллллллл  22.07.2019 01:50
Втреугольнике mnp m= 35 градусов, n= 110 градусов . сделайте рисунок, найдите угол р и докажите, что данный треугольник является равнобедренным. укажите равные стороны в данном...
МаксимФадеев МаксимФадеев  22.07.2019 01:50
Чему равна площадь сектора с центральным углом 12 градусов круга радиусом 12 см...
6hh6h6h 6hh6h6h  13.06.2019 09:40
Преобразуйте выражения (а,b,c-векторы): 1) (2a+b)(a-3b) 2) (a-b)(a--b)(b-c) 3)c(a+c)-a(a+c)...
404ada505 404ada505  13.06.2019 09:40
Как найти периметр выпуклого и не выпуклого четырехугольника , пятиугольника , шестиугольника? ? надо ! зорание...
sashakO5класс sashakO5класс  13.06.2019 09:40
Бессектрисы углов а и d параллелограмма abcd пересекаются в точке m, лежащей на стороне bc. найдите стороны параллелограмма, если его периметр 36 сантиметров....
alexandrvseznaika alexandrvseznaika  22.11.2020 23:06
Знайдіть площу трапеції ABCD, якщо BC= 3 см, AD= 12см, AC=13 см, BD=14 см...
Dаniеll Dаniеll  22.11.2020 23:06
Вычисли площадь ромба, если его сторона равна 18 см, а проведённая к ней высота равна 15 см. ответ: площадь ромба равна см2. ответить!...
царапина123 царапина123  22.11.2020 23:05
6. Знайдіть площу трикутника зі сторонами 16см та 13см та кутом 150° між ними...

Популярные вопросы