Нужно составить две на подобие треугольников, 8 класс. сама + дано + решение. 100 первому, кто ответит заранее

Ответы

maria610 09.10.2020 23:25

1. Треугольники АВС и MNK подобны. ∠А = ∠М. ВС = 8, NK = 2. Площадь треугольника MNK равна 12 (ед²). Найдите площадь треугольника АВС.- - -

Дано :

ΔАВС ~ ΔMNK.

∠А = ∠М.

ВС = 8.

NK = 2.

S(ΔMNK) = 12 (ед²).

Найти :

S(ΔABC) = ?

В подобных треугольниках против равных углов лежат сходственные стороны.

Отсюда стороны ВС и NK - сходственные.

Отношение сходственных сторон равно коэффициенту подобия.

То есть -

$\frac{BC}{NK} = k\\\\\frac{8}{2} = k\\\\ \boxed{k = 4}$

Но заметить, ища коэффициент подобия, я ставила в числитель элемент бóльшего треугольника. Поэтому при дальнейших расчётах, я буду также ставить элементы/площадь бóльшего треугольника в числитель.

Площади подобных треугольников относятся как квадрат коэффициента подобия.

Отсюда -

$\frac{S(\triangle ABC) }{S(\triangle MNK)} = k^{2} \\\\\frac{S(\triangle ABC) }{12} = 4^{2} \\\\\frac{S(\triangle ABC) }{12} =16\\\\S(\triangle ABC)=16*12=192\\$

192 (ед²).

- - -2. В треугольнике АВС отрезок MК (М ∈ АВ, К ∈ ВС) параллелен АС. МК = 14, АС = 42. Периметр треугольника МВК равен 32. Найдите периметр треугольника АВС.- - -

Дано :

ΔАВС.

М ∈ АВ, К ∈ ВС.

МК ║АС.

МК = 14.

АС = 42.

Р(ΔМВК) = 32.

Найти :

Р(ΔАВС) = ?

В треугольнике параллельный одной из сторон треугольника отрезок, пересекающий две другие стороны треугольника в точках, отсекает от данного треугольника подобный треугольник.

Отсюда -

ΔАВС ~ ΔMBK.

В подобных треугольниках против равных углов лежат сходственные стороны. И их же отношение равно коэффициенту подобия.

∠В - общий для ΔАВС и ΔMBK.

Отсюда стороны МК и АС - сходственные.

Тогда -

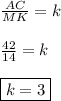
$\frac{AC}{MK} = k\\\\\frac{42}{14} = k\\\\ \boxed{k=3}$