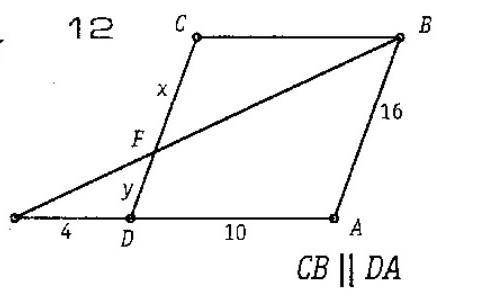
нужно найти x и y при подобия треугольников​

Добрый день! Давайте разберемся вместе с этим заданием.

У нас даны два подобных треугольника с вершинами A, B и C, которые обозначены на изображении. Подобные треугольники имеют одинаковые формы, но могут иметь разные размеры.

Обозначим стороны треугольников так: AC - x, BC - y, AB - h (дана в задании).

Для решения задачи, мы можем выразить соотношение сторон одного треугольника через стороны другого треугольника:

x/y = h/BC

Теперь подставим известные значения:

x/y = 5/7

Мы можем решить данное уравнение относительно x или y, если мы найдем одну из неизвестных величин.

Давайте найдем x.

Мы знаем, что сумма всех углов в треугольнике равна 180 градусам. В треугольниках ABC и ACD (рисунок), углы C и C1 соответственно, являются вертикальными углами и поэтому равны.

Таким образом, ∠C = ∠C1.

Из подобия треугольников, мы знаем, что ∠C1 = ∠B1.

А теперь вернемся к треугольнику AB1C1. Мы видим, что ∠C1 + ∠B1 + ∠AB1 = 180 градусов (сумма всех углов).

Подставим известные значения:

∠C1 + ∠B1 + 90 = 180

∠C1 + ∠B1 = 90

Теперь мы знаем, что ∠C1 + ∠B1 = 90 градусов.

Поскольку ∠C1 = ∠B по подобию треугольников, мы можем записать:

∠B1 + ∠B = 90

Теперь мы получили, что ∠B1 + ∠B = 90 градусов.

Таким образом, ∠B1 = 90 - ∠B.

Из подобия треугольников, мы также знаем, что стороны AD и DC относятся так же, как стороны AB и B1C1 (в подобии, стороны соответствующих углов пропорциональны).

Теперь мы можем записать:

AD/DC = AB/B1C1 = h/y

Подставим известные значения:

2/7 = 5/y

Таким образом, у нас есть уравнение:

2/7 = 5/y

Теперь мы можем решить это уравнение, чтобы найти y:

2y = 7 * 5

2y = 35
y = 35 / 2
y = 17.5

Таким образом, y = 17.5.

Используя полученное значение y, мы можем найти x, подставив значения в исходное уравнение:

x/y = 5/7

x/17.5 = 5/7

7x = 17.5 * 5

7x = 87.5

x = 87.5 / 7

x = 12.5

Таким образом, x = 12.5.

Ответы: x = 12.5 и y = 17.5.

Надеюсь, что объяснение было подробным и понятным для вас. Если возникнут другие вопросы, не стесняйтесь задавать.