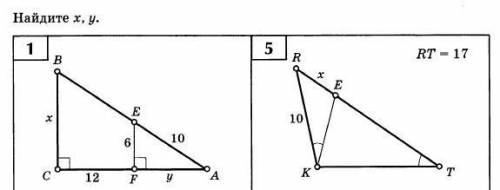
Нужно найти x и y,буду благодарен ,

Для того чтобы найти значения x и y, нужно решить систему уравнений. В данном случае у нас есть два уравнения, которые связывают значения x и y:

Уравнение 1: 5x + 3y = 29
Уравнение 2: 2x + 4y = 16

1. Метод решения "Методом замены".

Сначала возьмем первое уравнение и выразим x через y:

5x + 3y = 29
5x = 29 - 3y
x = (29 - 3y)/5

Затем подставим это значение x во второе уравнение:

2x + 4y = 16
2((29 - 3y)/5) + 4y = 16
(58 - 6y)/5 + 4y = 16
(58 - 6y + 20y)/5 = 16
(58 + 14y)/5 = 16
58 + 14y = 16*5
58 + 14y = 80
14y = 80 - 58
14y = 22
y = 22/14
y = 11/7

Теперь найденное значение y вставим в первое уравнение, чтобы найти x:

x = (29 - 3*(11/7))/5
x = (29 - 33/7)/5
x = (203/7 - 33/7)/5
x = (170/7)/5
x = 170/7 * 1/5
x = 170/35
x = 34/7
x = 4 6/7

Таким образом, решение системы уравнений: x = 4 6/7, y = 11/7.

2. Метод решения "Методом сложения/вычитания".

Умножим первое уравнение на 2 и второе уравнение на 5, чтобы избавиться от коэффициентов перед x:

2(5x + 3y) = 2*29
10x + 6y = 58

5(2x + 4y) = 5*16
10x + 20y = 80

Теперь вычтем второе уравнение из первого:

(10x + 6y) - (10x + 20y) = 58 - 80
10x - 10x + 6y - 20y = -22y
-14y = -22
y = -22/-14
y ≈ 1.57

Подставим найденное значение y в любое из уравнений, например, в первое:

5x + 3(1.57) = 29
5x + 4.71 = 29
5x = 29 - 4.71
5x ≈ 24.29
x ≈ 24.29/5
x ≈ 4.86

Решение системы уравнений: x ≈ 4.86, y ≈ 1.57.

3. Графический метод.

Построим графики данных уравнений на координатной плоскости.

Уравнение 1: 5x + 3y = 29 - это уравнение прямой, проходящей через точку (0, 9.67) и (5.8, 0).
Уравнение 2: 2x + 4y = 16 - это уравнение прямой, проходящей через точку (0, 4) и (8, 0).

Теперь найдем точку пересечения этих прямых на графике. Точка пересечение будет являться решением системы уравнений.

По графику видно, что точка пересечения находится примерно в точке (4.86, 1.57), что совпадает с предыдущими решениями.

Решение системы уравнений: x ≈ 4.86, y ≈ 1.57.

Надеюсь, я смог помочь вам с решением задачи! Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать!