Нужно доказать что если она в два раза основания и параллельна AC то она является средней линией
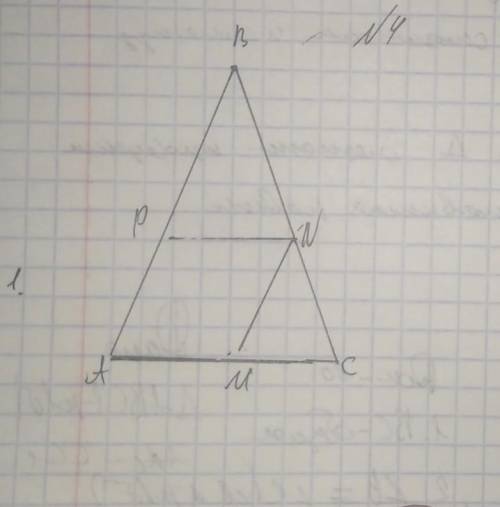
Другие вопросы по теме Геометрия
Популярные вопросы
- Данная развертка является разверткой какой геометрической фигуры?...
2 - Аллегория в басне волк и ягнёнок НАДО ОЧЕНЬ...
2 - Один рассказ из цикла Колымские рассказы В.Шаламова (рекомендую Шерри...
2 - В настоящее время господствующей группой растений на планете являются...
3 - выполни те с решением. за все выполненные задания...
3 - Найти однородные члены предложения и составить к ним схемы...
3 - Перед вами описание экосистемы.Экосистема хвойного леса формируется...
2 - Задание. Напишите эссе на предложенную тему «Как убедить людей беречь...
3 - загадки придумать к словам 1) Блик 2) мольберт3) графика 4) мазок...
2 - Исследовательница В.Ф.Соколова утверждает, что необычность Наташи...
2
Объяснение:
Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника. Средняя линия треугольника параллельна третьей стороне и равна ее половине
Т.к. РN ║AC , то ΔАВС и ΔPBN подобны по 3-м углам. Следовательно,
АС : PN = AB : PB = BC : BN
Но PN : AC = 1 : 2 (по условию), значит, и
AB : PB = BC : BN = 1 : 2, тогда
АВ = 2 РВ и ВС = 2ВN, т.е. PN делит стороны АВ и ВС пополам. Следовательно, РN - средняя линия ΔАВС, ч.т.д.