но надо писать не только ответ,но и решение. P.S.Кто умничит и будет писать что-то другое,дам жалобу и его(её) акк забанят.
Другие вопросы по теме Геометрия
Популярные вопросы
- Вми бимоль мажоре построить главные трезвучие с обращениями...
2 - Значение живых организмов в жизни человека положительная и отрицательная...
1 - Составьте квадратное уравнение, если известны их коэффиценты а=-3, b=5,...
2 - Ссклоняется ли слово рассечь по падежам если да то можно примеры...
1 - Рассчитайте по уравнению 2zn+o2 = 2zno какой объем кислорода необходим...
2 - Задай вопросы. kate waters the flowers every sunday....
3 - Сопоставьте стихотворение м.ю. лермонтова «нет, не тебя так пылко я...
1 - Mb- перпендикуляр проведенный из точки m к плоскости альфа , а ma mc...
1 - Найдите дополнение, обстоятельство, сказуемое, подлежащее, определение...
1 - Моторний човен проходить шлях за течією від а до в за 4 год. , а зворотній...
3
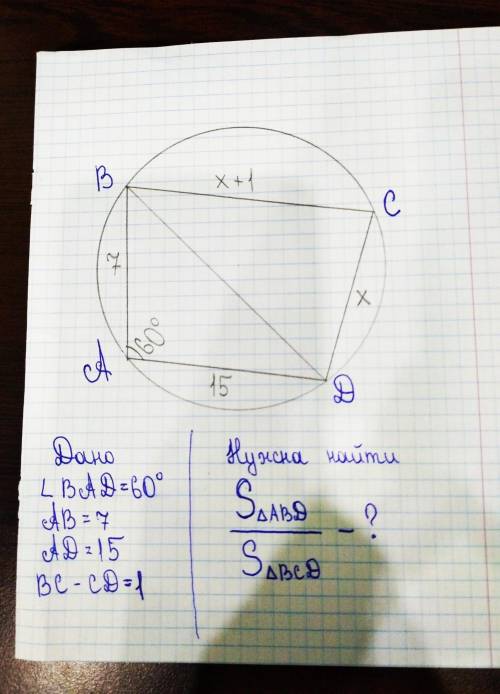
по т косинусов найду BD
BD^2=AB^2-AD^2-2*AB*AD*cos<A=7^2+15^2-2*7*15*0.5=274-105=169=13^2
BD=13
У вписанного четырехугольника суммы противоположных углов 180 °
<C=180-<A=180-60=120°
Тогда по той же теореме выражу BD из ΔBCD
BD^2=BC^2+CD^2-2*BC*CD*cos<C
169=(x+1)^2+x^2-2x(x+1)*cos120
169=x^2+2x+1+x^2-2x(x+1)(-0.5)
169=2x^2+2x+1+x^2+x
169=3x^2+3x+1
3x^2+3x-168=0-делю на 3
x^2+x-56=0
D=1+224=225=15^2
x=(-1+15)/2=7
Тогда CD=7;BC=8
S(ABD)=0.5AB*AD*sin<A=0.5*7*15*√3/2=105√3/4
S(BCD)=0.5*BC*CD*sin<C=0.5*8*7*sin120=56√3/4
S(ABD)/S(BCD)=105/56
C =180-A =120 (вписанный четырехугольник)
CD=x, BC=x+1
Теорема косинусов для BCD и ABD
BD^2 =x^2 +(x+1)^2 -2x(x+1) cos120 =7^2 +15^2 -2*7*15 cos60 =>
3x^2 +3x +1 =169 => x^2 +x =168/3 =56
S(ABD)/S(BCD) =7*15 sin60 / x(x+1) sin120 =7*15/56 =15/8