1. Геометрия
  2. Nnnlll54 ! 20 ! в прямоугольном

Nnnlll54 ! 20 ! в прямоугольном треугольнике abc(c=90), высота ch=7, биссектриса = 35/4. найти катеты и площадь abc.

ArtimonТёма22887 ArtimonТёма22887    3   03.10.2019 10:20    2

Ответы
панда1341 панда1341  09.10.2020 13:52

ΔАВС , ∠С=90° , СК- биссектриса  ⇒ ∠АСК=∠ВСК=45° , СН⊥АВ  ⇒  ∠СНВ=90°, СН=7 ,  СК=35/4 .

Рассм. ΔСКН - прямоугольный. Обозначим ∠КСН=α  ,

КН=√(СК²-СН²)=√((35/4)²-7²)=√(441/16)=21/4 .

tgα=КН/СН=21/4:7=3/4 .

Рассм. ΔВСН. ∠ВСН=∠ВСК-∠КСН=45°-α  ⇒  ∠В=90°-(45°-α)=45°+α .

tg∠ВСН=tg(45°-α)=ВН/СН  ⇒  ВН=СН·tg(45°-α)=7·tg(45°-α) .

tg(45^\circ -\alpha )=\frac{tg45^\circ -tg\alpha }{1+tg45^\circ \cdot tg\alpha }=\frac{1-3/4}{1+3/4}=\frac{4-3}{4+3}=\frac{1}{7}

BH=7\cdot \frac{1}{7}=1

BC=\sqrt{BH^2+CH^2}=\sqrt{1^2+7^2}=\sqrt{50}=5\sqrt2

Рассм. ΔАСН. ∠АСН=∠АСК+∠КСН=45°+α .

tg∠АСН=АН/СН  ⇒  АН=СН·tg∠АСН=7·tg(45°+α)

tg(45^\circ +\alpha )=\frac{tg45^\circ +tg\alpha }{1-tg45^\circ tg\alpha }=\frac{1+3/4}{1-3/4}=\frac{4+3}{4-3}=7\\\\AH=7\cdot 7=49\\\\AC=\sqrt{AH^2+CH^2}=\sqrt{7^2\cdot tg^2(45^\circ +\alpha )+7^2}=7\sqrt{49+1}=\\=7\cdot \sqrt{50}=35\sqrt2\\\\AB=AH+HB=49+1=50\\\\S(ABC)=\frac{1}{2}\cdot AB\cdot CH=\frac{1}{2}\cdot 50\cdot 7=175

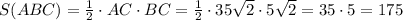Или:  S(ABC)=\frac{1}{2}\cdot AC\cdot BC=\frac{1}{2}\cdot 35\sqrt2\cdot 5\sqrt2=35\cdot 5=175  .


Nnnlll54 ! 20 ! в прямоугольном треугольнике abc(c=90), высота ch=7, биссектриса = 35/4. найти катет
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
KageyamaT KageyamaT  21.01.2021 15:24
Номер 566, малюнок 164. До ть будь ласка!...
squeezy1312 squeezy1312  21.01.2021 15:24
В треугольнике DEF ∠D = 2∠F, ∠D – ∠E = 30°. Найди ∠D, ∠E, ∠F....
burch123 burch123  21.01.2021 15:24
Точка L належить стороні BC трикутника ABC. Чи є AL бісектрисою трикутника, якщо: а) АВ = 12 см, AC = 15 см, ВС = 18 см, BL = 8 см; б) АВ = 10 см, AC = 16 см, BL: LC = 5:7....
nikzyryanov02 nikzyryanov02  21.01.2021 15:23
Відрізок BM — медіана трикутника ABC із вершинами A (3; –5), B (2; –3) і C (–1; 7). Знайдіть координати та модуль вектора BM...
pRoToTyPe95wF pRoToTyPe95wF  30.01.2021 09:43
№1. По рисунку 1. АВСD – трапеция. Найдите длину нижнего основания трапеции, если АВ = 10, ВК = 4, ВС = 6....
АнгелинаМанакова АнгелинаМанакова  30.01.2021 09:46
Дан треугольник ABC, на стороне AC которого взята точка D такая, что AD=5 см, а DC=13 см. Отрезок DB делит треугольник ABC на два треугольника. При этом площадь треугольника ABC составляет...
Fyzelen Fyzelen  30.01.2021 09:46
Доказать, что треугольник ABC равнобедренный​...
АнастасияКот26 АнастасияКот26  30.01.2021 09:53
№2. По рисунку 2. АВСD – параллелограмм. Найдите длину стороны ВС, если ВО = 6, МО = 4, ОD = 5....
камила507 камила507  25.01.2021 23:31
Використавши властивість бісектриси трикутника, знайдидовжину відрізка мс. Якщо МС, Х2 стороны 10 и 6 а бисектриса делит низ треугольника на 8 и Х​...
Nastya7654321 Nastya7654321  25.01.2021 23:32
Дано (x-4)²+y²=16,коло.Знайти центр кола -О і радіус.Повний розв язок​...

Популярные вопросы