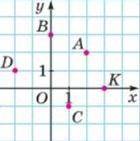
Назовите точку, ордината которой равна нулю C
B
A
K
Вопрос №2
В какой четверти лежит точка A(x;y), если x>0, y<0?

II
III
I
IV
Вопрос №3
Расстояние между точками A(x;3) и B(1;-5) равно 10. Найдите x.

7 или -5
-5
7
-7 или 5
Вопрос №4
Найдите координаты точки, которая принадлежит оси ординат и равноудалена от точек D(-2;-3) и E(4;1)

Невозможно определить
(0;1)
(0;0,5)
(1/3;0)
Вопрос №5
Найдите длину отрезка, концы которого принадлежат осям координат, а серединой является точка M(-3;8)

16
6
2√73
292

Назовите точку, ордината которой равна нулю C B A K Вопрос №2 В какой четверти лежит точка A(x;y),

Ответы

34234252 25.11.2021 21:57

$\sqrt{8}$ ответ:

1. К

2. IV

3. 7 или -5

4. (0;0,5)

5. 2√73

6. (3√3; 1) или (-3√3; 1)

7. ромб

Объяснение:

1. Координаты точки К (3;0)

2. Координаты x>0, y<0 могут быть только в IV четверти

3. АВ=10=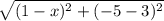 $\sqrt{(1-x)^{2}+(-5-3)^{2} }$ Приводим к квадратному уравнению 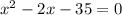$x^{2} -2x-35=0$ . Решаем через дискриминант и получаем х1=7, х2=(-5)

4. Координаты этой точки, допустим М (0;у) Нужно найти у. Поскольку эта точка М равноудалена от точек Д и Е, то расстояние между ними одинаковое, то есть по формуле расстояния между точками находим расстояния между ДМ и ЕМ и приравниваем. Решаем уравнение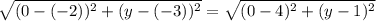 $\sqrt{(0-(-2))^{2}+(y-(-3))^{2} } =\sqrt{(0-4)^{2}+(y-1)^{2} }$ и получаем у=0,5

5. Координаты точек А(х;0), В(0;у) В формулу середины отрезка подставляем эти координаты и координаты точки М(-3;8): (-3)=(х+0)/2 х=(-6); 8=(0+у)/2 у=16. Теперь по формуле расстояния между точками находим расстояние между точками АВ и получаем АВ=2√73

6. Вершина В может быть или в 1й четверти, или во 2й четверти. По формуле расстояния между точками находим расстояние между точками А и С. Получаем 6. Поскольку ABC равносторонний треугольник, то АС=АВ=ВС=6. По формуле расстояния между точками находим расстояния между АВ и ВС и приравниваем. Решаем уравнение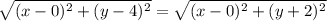 $\sqrt{(x-0)^{2}+(y-4)^{2} } = \sqrt{(x-0)^{2}+(y+2)^{2} }$ и получаем у=1.

Подставляем значение у=1 в любую из сторон уравнения и получаем х1= 3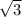 $\sqrt{3}$ , х2= -3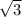 $\sqrt{3}$

7. Если высчитать расстояние между точками, то есть стороны четырехугольника, то они равны: АВ=ВС=СД=АД=2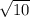 $\sqrt{10}$ . То есть это либо ромб, либо квадрат. Дальше высчитываем длину диагоналей тоже как расстояние между точками: АС=2 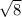$\sqrt{8}$ , ВД=4 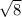$\sqrt{8}$ . То есть диагонали не равны, значит это не квадрат, а ромб.