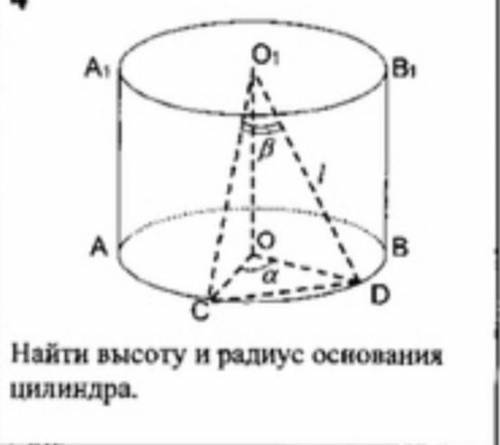
Найти высоту и радиус основания цилиндра

Для решения данной задачи, нам необходимо использовать знания о свойствах и формулах для цилиндра.

Цилиндр - это трехмерное геометрическое тело, в котором две основания представляют собой параллельные круги, а боковая поверхность соединяет эти основания.

Задача требует найти высоту и радиус основания цилиндра. Для этого нужно использовать формулы, связывающие объем и площадь боковой поверхности цилиндра с высотой и радиусом его основания.

1. Поиск высоты цилиндра:
Высота цилиндра обозначается буквой "h". Для нахождения высоты, нам необходимо воспользоваться теоремой Пифагора.

Так как цилиндр имеет форму прямого кругового конуса, в котором высота равна пирамиде, лежащей на такой базе, то можем записать уравнение:
h^2 = r^2 + l^2,

где r - радиус основания цилиндра, l - образующая цилиндра. Образующая представляет собой отрезок, соединяющий вершину цилиндра с центром одного из его оснований.

В данном случае, у нас нет информации об образующей, но у нас есть информация о площади боковой поверхности цилиндра, которую мы можем использовать для нахождения образующей.

2. Поиск радиуса основания цилиндра:
Радиус основания цилиндра обозначается буквой "r". Для нахождения радиуса, нам необходимо использовать формулу для площади боковой поверхности цилиндра.

Площадь боковой поверхности цилиндра выражается следующей формулой:
Sбп = 2πrh,

где Sбп - площадь боковой поверхности цилиндра, π - число "пи" (примерно равно 3.14), r - радиус основания цилиндра, h - высота цилиндра.

У нас есть значение площади боковой поверхности цилиндра, и мы можем использовать эту формулу для нахождения радиуса.

Теперь перейдем к решению задачи:
1. Поиск высоты цилиндра:
У нас есть формула для высоты цилиндра: h^2 = r^2 + l^2.

Из геометрических свойств цилиндра, мы знаем, что образующая является прямым отрезком, соединяющим центр одного из оснований цилиндра с вершиной цилиндра. Так как в данной задаче нет информации о длине образующей, мы не сможем найти высоту цилиндра без дополнительной информации.

2. Поиск радиуса основания цилиндра:
У нас есть формула для площади боковой поверхности цилиндра: Sбп = 2πrh.

Мы также имеем значение площади боковой поверхности цилиндра (в данном случае в задаче нет конкретного значения площади), и нам необходимо записать уравнение с известными значениями и неизвестным радиусом r.

3. Уравнение для нахождения радиуса:
Sбп = 2πrh.

Заменяем известные значения на переменные и получаем уравнение:
Sбп = 2πrh,
где Sбп - площадь боковой поверхности цилиндра, π - число "пи" (примерно равно 3.14), r - радиус основания цилиндра, h - высота цилиндра.

Это уравнение содержит две переменные (r и h), поэтому нужно иметь больше информации или уравнений, чтобы решить его и определить эти значения.

В итоге, без дополнительной информации или уравнений невозможно найти высоту и радиус основания цилиндра.