Найти уравнение прямой, проходящей через вершину В и параллельной медиане АМ треугольника

mishakukla 1 05.12.2021 00:15 1

Question

Геометрия: Найти уравнение прямой, проходящей через вершину В и параллельной медиане АМ треугольника

mishakukla · Answer

Вершины треугольника А(2;0) , В(5;3) , С(3;7). Найдите уравнение прямой, проходящей через вершину В и параллельной медиане АМ треугольника

Объяснение:

Пусть прямая , проходящая через точку В будет m. Тк m ║ AM, то у прямых одинаковое к.

1) Ищем уравнение прямой АМ.

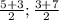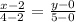Первая точка А(2;0), вторая М( $\frac{5+3}{2} ;\frac{3+7}{2}$ ) или М(4;5) : $\frac{x-2}{4-2} =\frac{y-0}{5-0}$ ⇒

5(x-2)=2y или у=2,5х-5 ⇒ к(АМ)=2,5 и тогда к(m)=2,5.

2)Прямой у=кх+b принадлежит точка В(5;3) и к=2,5 :

3=2,5*5+b ⇒ b=-9,5. Получили у=2,5х-9,5

=================

Формула для вычисления координат середины отрезка х=(х₁+х₂):2 ,

у=(у₁+у₂):2 где (х₁;у₁), (х₂;у₂) координаты концов отрезка , (х;у )-координаты середины.

Если прямая проходит через точки М1(х1; у1) и М2(х2; y2) то уравнение прямой (x - x1)/(x2 - x1) = (y - y1)/(y2 - y1). orjabinina

Найти уравнение прямой, проходящей через вершину В и параллельной медиане АМ треугольника