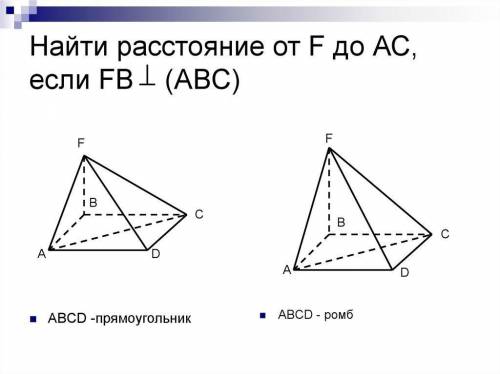
Найти расстояние от F до AC 1) если FB перпендикулярна (ABC), ABCD-прямоугольник
2) если ABCD-ромб

Добрый день! Давайте рассмотрим оба варианта по очереди. 1) Когда ABCD - прямоугольник: Мы видим, что треугольник FBC является прямоугольным, так как FB перпендикулярна к ABC. Поэтому мы можем воспользоваться теоремой Пифагора для вычисления расстояния от F до AC. Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. В нашем случае, катеты треугольника FBC - это FB (высота) и FC (проекция AC на ось X). Тогда расстояние от F до AC (обозначим его как d) будет равно: d^2 = FB^2 + FC^2. Для вычисления FB и FC, нам нужно разделить рассмотрение треугольника на две части - прямоугольный треугольник ABC и треугольник ABCD. - Высота FB в треугольнике ABC: Мы можем видеть, что треугольник ABC является прямоугольным, поэтому сторона AB является высотой, опущенной из вершины B на сторону AC. Длина стороны AB равна 3 см. - Проекция AC на ось X (длина FC) в треугольнике ABCD: Мы знаем, что ABCD - прямоугольник, поэтому его боковые стороны параллельны. Значит, сторона AC (и ее проекция FC на ось X) равна 6 см. Теперь мы можем приступить к вычислению расстояния d: d^2 = FB^2 + FC^2. d^2 = 3^2 + 6^2. d^2 = 9 + 36. d^2 = 45. d ≈ √45. d ≈ 6.71 см. Таким образом, расстояние от F до AC в прямоугольнике ABCD составляет примерно 6.71 см. 2) Когда ABCD - ромб: Мы видим, что треугольник FBC также является прямоугольным, так как FB перпендикулярна к ABC. Поэтому для вычисления расстояния от F до AC можно использовать ту же самую теорему Пифагора. Однако, в ромбе ABCD диагонали равны и пересекаются под прямым углом, то есть BO и FC являются диагоналями ромба. Значит, FB является половиной диагонали BO. Длина диагонали BO ромба ABCD равна длине стороны AB, то есть 3 см. Тогда длина FB будет: FB = 1/2 * BO = 1/2 * 3 = 1.5 см. Теперь мы можем снова использовать теорему Пифагора для вычисления расстояния d: d^2 = FB^2 + FC^2. d^2 = 1.5^2 + 6^2. d^2 = 2.25 + 36. d^2 = 38.25. d ≈ √38.25. d ≈ 6.19 см. Таким образом, расстояние от F до AC в ромбе ABCD составляет примерно 6.19 см. Надеюсь, это решение понятно для вас! Если у вас возникнут еще вопросы, буду рад помочь.