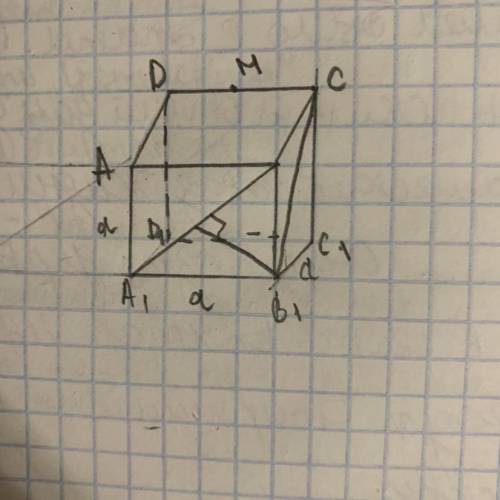
Найти расстояние между скрещивающимися диагоналями двух соседних граней куба с ребром а.

Добрый день! Для начала разберемся с некоторыми понятиями, чтобы понять условие задачи.

Куб - это геометрическое тело, имеющее шесть граней, все из которых являются квадратами. В нашем случае, грани куба будут выглядеть как на картинке - у нас есть две соседние грани, красная и синяя.

У куба есть три оси симметрии, относительно которых можно поворачивать куб на 90 градусов. Одна из таких осей симметрии проходит по диагонали грани куба (это диагональ, которую мы ищем). Как видно на картинке, эта диагональ будет иметь длину а.

Чтобы найти расстояние между скрещивающимися диагоналями двух соседних граней куба, нам нужно найти длину отрезка, который соединяет две скрещивающиеся диагонали.

Давайте разберемся, где находится этот отрезок на картинке. Мы видим, что он проходит через центр куба и состоит из противоположных углов каждой из соседних граней. Давайте обозначим эти две противоположные грани как A и B.

Теперь самое интересное. Мы знаем, что внутри куба есть диагональ, которая соединяет два противоположных его угла (такая диагональ есть в каждой грани куба). Давайте обозначим эту диагональ грани A как D1, и диагональ грани B как D2.

Так как все грани куба являются квадратами, то каждая диагональ грани равна длине ребра умноженной на √2. В нашем случае длина ребра куба равна а, так что D1 = D2 = a√2.

Теперь, чтобы найти расстояние между скрещивающимися диагоналями, нам нужно найти длину отрезка диагонали куба, который соединяет точки D1 и D2. Такой отрезок называется "скрещивающейся диагональю".

Давайте обозначим эту скрещивающуюся диагональ как D. Используя теорему Пифагора для треугольников D1, D2 и D, мы можем найти ее длину.

Теорема Пифагора утверждает, что в прямоугольном треугольнике, квадрат длины гипотенузы (самой длинной стороны треугольника) равен сумме квадратов длин двух других сторон.

Итак, применяя теорему Пифагора к треугольнику D1-D-D2, у нас получается следующее:

D^2 = D1^2 + D2^2.

Подставляя значения для D1 и D2, получаем:

D^2 = (a√2)^2 + (a√2)^2.

Это можно упростить следующим образом:

D^2 = 2a^2 + 2a^2.

D^2 = 4a^2.

Теперь избавимся от квадрата, взяв квадратный корень с обеих сторон:

D = 2a.

Таким образом, расстояние между скрещивающимися диагоналями двух соседних граней куба с ребром а равно 2a.

Надеюсь, мой ответ был понятен и подробен. Если у тебя возникли еще вопросы, пожалуйста, задай их. Я буду рад помочь!