1. Геометрия
  2. Найти площадь ромба если известно

Найти площадь ромба если известно что сторона равна одной из его диагоналей и равна 8 корней из 3

AgafAl AgafAl    2   16.03.2019 00:30    0

Ответы
maloy4424 maloy4424  25.05.2020 14:41

Есть формула что сторона ромба(a) равна

4a^{2}=d1^{2}+d2^{2}<span\\</span

 

4a^{2}=a^{2}+d2^{2}\\ 3a^{2}=d2^{2}\\

 

3*64*3=d2^{2} d2=24

 

Sромба=(1/2)*d1*d2=1/2*8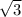\sqrt{3}*24=96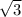\sqrt{3}

 

ПОКАЗАТЬ ОТВЕТЫ
26271123 26271123  25.05.2020 14:41

Сторона ромба с половинками диагоналей образует прямоугольный треугольник. Итак, имеем прямоугольный треугольник со сторонами 8 корней из 3 (гипотенуза) и 4 корня из 3 (один из катетов). Найдём второй катет: корень из (192 - 48) = 12.

Следовательно, вторая диагональ ромба равна 12 * 2 = 24.

Площадь ромба равна половине произведения его диагоналей.

S = (8 корней из 3 * 24) / 2 = 96 корней из 3.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
alina2015a alina2015a  03.09.2019 07:30
Составьте уравнение прямой, проходящей через точку в (-3; 8) и образует с положительным направлением оси абсцисс угол 135 °...
yuliana080704 yuliana080704  03.09.2019 07:30
Катет прямокутного трикутника відноситься до гіпотенузи як 5: 13.знайти периметр трикутника ,якщо його другий катет дорівнює 24 см....
mihaikl mihaikl  19.04.2019 12:15
Основание пирамиды -ромб с диагоналями 6 и 8 см . высота пирамиды опущена в точку пересечения его диагоналей. меньшие боковые ребра пирамиды равны 5 см найди объем пирамиды...
Taynik Taynik  19.04.2019 12:10
Необходимо найти площадь треугольника nok​...
nazuli nazuli  19.04.2019 12:07
Шар с центром в точке о касается плоскости в точке а. точка б лежит в плоскости касания. найдите объем шара если ab-=15см, bo=17см...
Король344 Король344  19.04.2019 12:07
Уяку точку переходить точка с(-3; 4) при паралельному перенесені, що переводить точку а(0; 5) у точкув(3; -1)...
master204 master204  28.05.2019 15:00
Найдите площадь прямоугольника, если его периметр равен 44 к один, сторона на 2 больше другой. это к гиа...
corbaov2018 corbaov2018  28.05.2019 15:00
Две медианы треугольника равны 3 см и 6 см, а одна из сторон 8 см. найти меньшую сторону треугольника...
нурана4 нурана4  28.05.2019 15:10
Укажите номера верных утверждений. 1) через любую точку проходят не менее одно прямой. 2) если при пересечение двух прямых третьей прямой соотвественные углы равны 65 , то...
Uhbif627 Uhbif627  08.10.2019 00:10
Найти углы треугольника если известно что один угол в два раза меньше второго угла и на 60° меньше третьего угла? !...

Популярные вопросы