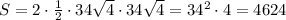Найти площадь ромба, если его сторона равна 34√4, острый угол равен 60°.
Другие вопросы по теме Геометрия
Популярные вопросы
- Выделение квадрата двучлена из квадратного трёхчлена. напишите примеры)...
1 - El o c m w e o t c s h o l o -составить из этих букв предложение...
2 - 1)- я приближался к месту моего назначения. 2)- мужичок тут же стал его тулуп примеривать....
2 - Які переваги дає висока впорядкованість біологічний системам?...
2 - Какие приборы ( инструменты) , по твоему мнению , вести длительное наблюдение за...
2 - Белок состоит из 100 аминокислотных остатков и имеет следующий состав: 40% глицина,...
3 - ответить на вопрос, меня гугл глючит не могу 1)объясните,какие особенности строения...
1 - Возникновение человека и общества - процессы, неразрывно связанные друг с другом....
2 - Черные, кривые встанут в ряд- заговорят....
3 - Сөз тіркестерін,тұрақты тіркестерді және күрделі сөздерді бөлек-бөлек топтап жазыңдар....
2
Поделим ромб пополам на два треугольника. Они равны между собой по двум сторонам и углу между ними.
У каждого из треугольников две стороны равны по определению ромба, а следовательно треугольники равнобедренные. Т.к. острый угол треугольника равен 60°, а два другие угла равны между собой, то они равны 120°/2 =60°. Т.е. ромб состоит из двух равных равносторонних треугольников.
Тогда площадь робма равна: