Найти площадь прямоугольного треугольника со сторонами, равными  3, 4  и 5 ед.длины
​

Первый

Если это прямоугольный треугольник, то квадрат гипотенузы равен сумме квадратов катетов, исходя из его свойств. Нужно понять, какие единицы являются длинами катетов.

Если рассмотреть каждый случай, то очевидно, что длина катета равна 5(3²+4²=5², остальные равенства не выполняются).

Площадь прямоугольного треугольника равна половине произведения катетов

S =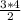 = 6

Есть второй через формулу Герона

Зная 3 стороны треугольника, найдём его полупериметр

p = 1/2 P = 1/2 (a+b+c) = 1/2 (3+4+5) = 12/2 =6

Формула Герона

S =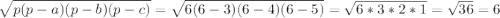

ответ: 6