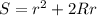Найти площадь прямоугольного треугольника, если известно, что радиус вписанного в треугольник круга равен r, а описанного - r.
Другие вопросы по теме Геометрия
Популярные вопросы
- Пояснити, що таке розвиток з неповним перетворенням? Назвати приклади комах...
3 - Определите количество и мощность ламп накаливания, необходимых для общего...
2 - 628. Упростите выражение: 11) - 0,3 :а: 32) 2= .ь. (1)332183)х:(-2,5);te4)...
1 - Складові промислової революці...
2 - Read the story of Archimedes and his bath. Then complete the text with the...
2 - . Спишите предложения подчеркните в них грамматические основы и дополнения....
1 - Қаныш Сәтбаев аты не себепті бірнеше елмен байланысты? ...
1 - Масла массой 744 г от 11°С до 55°С сожгли 3,8 г керосина. Определи КПД (коэффициент...
2 - Централизованное распределение производимых благ и услуг, какая экономическая...
1 - Сумма двух углов образованных при пересечении двух параллельных прямых секущей...
1
Зная, что гипотенуза равна двум радиусам описанной окружности, запишем:
Добавим к обеим частям неравенства слагаемое 2аb и преобразуем его в правой части:
Так как площадь прямоугольного треугольник равна половине произведения его катетов, то:
Зная, что площадь треугольника равна половине произведения его периметр на радиус вписанной окружности, получим:
Подставим вместо а+b и с известные выражения:
Выполняем преобразования:
Возведем обе части в квадрат:
R² взаимно уничтожается, сокращаем на S:
Домножаем на r:
Площадь прямоугольного треугольника равна сумме удвоенного произведения радиусов вписанной и описанной окружности и квадрата радиуса вписанной окружности. (Или: площадь прямоугольного треугольника равна произведению радиуса вписанной окружности на сумму его же с диаметром описанной окружности)
ответ: 2Rr+r²
Для решения данной задачи воспользуемся такой теоремой:
Центр окружности описанной около прямоугольного треугольника, делит гипотенузу пополам.
Тогда имеем прямоугольный треугольник со сторонами:
Исходя из того что треугольник прямоугольный находим катеты:
Так как площадь прямоугольного треугольника равна: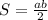
получаем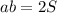
тогда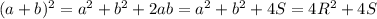
Получаем:
Зная, что площадь равна: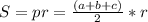
Получаем: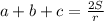
тогда получаем:
Прибавим с обеих сторон:
с обеих сторон:
т.к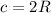 Получаем:
Получаем:
так как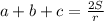
получаем:
Делим все на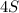 :
:
Откуда получаем:
ответ: