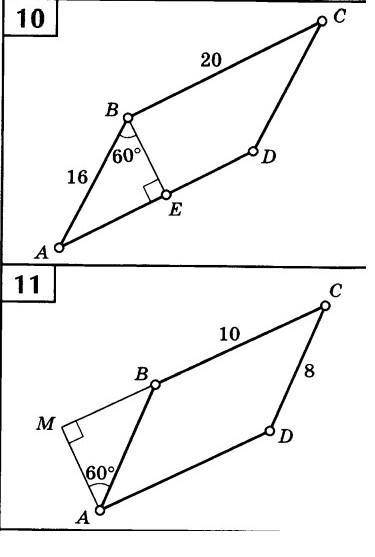
Найти площадь параллелограмма ABCD
Другие вопросы по теме Геометрия
Популярные вопросы
- фактический размер ядра клетки 15 мкм, размер изображения 1,5 см. вычислите...
2 - Ваза, тәрелке, шкаф қандай материалдардан жасалған?...
2 - Шамалардың қатынасын табыңдар ACB...
3 - Задание 2 найди в дополнительных источниках и дай определение ПОНЯТИЯМПолихромный...
3 - Периметр прямоугольника 22 см. Каковы размеры прямоугольника, если его длина...
2 - Пути большевистской модернизации причины модернизации...
1 - Заполните пропуски: Звуки речи ничем не отличаются от любых других звуков. Все...
1 - Определите кофицент и степень одночлена...
3 - № 1. Берілген сөйлемдерден көмекші есімдерді тауып көрсетіңіз. 1.Құнанбайдың...
1 - периметр треугольника АВС равен 20 см. Найдите периметр треугольника, вершинами...
2
10. Берём треугольник ABE. <A=30° (180-90-60), значит BE=1/2AB
Т.к. катет, лежащий напротив угла в 30°, равен 1/2 гипотенузы.
Значит BE=8
BC=AD по свой-вам параллелограмма, значит AD=20
Дальше формула площади параллелограмма.
a=AD
h=EB
Sпараллел.=20×8=160см²
11. Тоже самое. <B=30° (180-90-60), значит MA=1/2 гипотенузы. Гипотенуза = BA, а BA=CD (по свойствам параллелограмма)
BA=8 см
Значит 8:2=4
MA=4 см
AD=BC(по свойствам) =10
Та же формула. AD×MA
Sпараллел=10×4=40см²
10. S=ah
BC=AD=20
ΔABE прямоугольный
∠А=30° т.к сумма углов вΔ=180°
катет лежащий напротив ∠=30° равен половине гипотенузы
BE=16÷2=8
S=8*20=160
11. CD=AB=8
∠MBA=30° т.к сумма ∠ вΔ=180°
катет лежащий напротив угла =30° равен половине гипотинузы
АМ=8÷2=4 АМ- высота
S=ah
S=10*4=40
Объяснение: