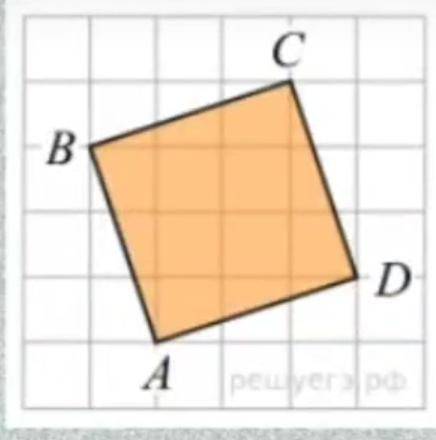
Найти площадь наклонного квадрата

По рисунку видно, что стороной квадрата является гипотенуза прямоугольного треугольника 3 на 1

По т. Пифагора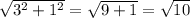

Площадь квадрата равна его стороне в квадрате

Чтобы найти площадь наклонного квадрата, нужно сначала разобраться в его основных свойствах. Наклонный квадрат - это фигура, у которой все стороны равны между собой, но углы, образованные сторонами, отличаются от прямого угла (90 градусов).

Для начала, давайте определим некоторые известные величины на картинке. Пусть сторона квадрата равна "a", а угол наклона равен "α".

Второе важное свойство, которое нам пригодится, это то, что сторона квадрата делится на две половины диагонали, образуя два прямоугольных треугольника.

Теперь давайте рассмотрим один из этих треугольников. Он прямоугольный, поэтому мы можем использовать теорему Пифагора, чтобы выразить один из катетов через гипотенузу. В нашем случае, гипотенуза равна "a", а катет, образующий угол "α", пусть будет "b".

Теорема Пифагора гласит:
гипотенуза² = катет₁² + катет₂²

Применим эту формулу к нашему треугольнику:
a² = b² + b²

Теперь, объединим эти два квадрата и сгруппируем слагаемые:
a² = 2b²

Далее, найдём катет "b" через тригонометрические функции. Обратите внимание, что катет "b" - это противолежащий катет для угла "α". Мы знаем, что тангенс угла "α" равен отношению противолежащего катета к прилежащему. Подставим значения в формулу:

tan(α) = b / a

Решим эту формулу относительно катета "b":
b = tan(α) * a

Теперь, подставим это выражение для "b" в выражение для площади:

a² = 2(tan(α) * a)²

Упростим это выражение:
a² = 2tan²(α) * a²

Для того, чтобы найти площадь квадрата, нужно знать его сторону "a". Однако, мы можем упростить это выражение, перенеся "a²" на одну сторону:
a² - 2tan²(α) * a² = 0

Факторизуем это выражение:
a²(1 - 2tan²(α)) = 0

Теперь, чтобы найти значение стороны "a", нужно решить это уравнение. Поскольку у нас есть произведение двух факторов, один из которых равен нулю, то мы можем приравнять каждый фактор к нулю и решить два уравнения:

1 - 2tan²(α) = 0
a² = 0

Первое уравнение не имеет решений, так как тангенс не может быть отрицательным. Второе уравнение говорит нам, что сторона квадрата равна нулю, что не является валидным результатом.

Из этих уравнений мы получаем, что площадь наклонного квадрата равна нулю.