1. Геометрия
  2. Найти периметр четырёхугольника,вершины

Найти периметр четырёхугольника,вершины которого есть серединами сторон квадрата,диаганаль которого 10 см.

eldardadashov eldardadashov    2   28.03.2019 04:40    0

Ответы
karinkaloseva2003 karinkaloseva2003  26.05.2020 21:33

если диагональ равна 10,

следовательно по теореме пифагора найдем стороны квадрата:

a^2 +a^2 =10^2

2a^2=100

a^2=50

a= 5\sqrt{2}

 

четырех угольник из условия будет являться квадратом, т.к. вписан в квадрат

 

найдем сторону этого прямоугольника:

\frac{a^2}{2} + \frac{a^2}{2} = b^2 (где b сторона искомого четырехугольника)

b^2=50

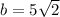
b= 5\sqrt{2}

  P= 4* 5\sqrt{2} = 20\sqrt{2}
ПОКАЗАТЬ ОТВЕТЫ
vk20001 vk20001  26.05.2020 21:33

сторона квадрата по диагонали равна корню квадратному из Д2:2=10*10:2=50=5V2

 

сторона нового квадрата (в) - гипотенуза в равнобедренном прямоугольном треугольнике со стороной а:2. Значит  в2=(а:2)2+(а:2)2=50:4+50:4=25, в=5

Р=4*5=20

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
llallallup llallallup  09.08.2019 10:16
Эта фигура не является многоугольником потому ,что сторона ab имеет общию вершину о с несмежной стороной cf? да и как это оформлять то есть потому ,что (несмежная сторона ab имеет...
almaz20004 almaz20004  09.08.2019 12:10
Расстояние от точки пересечения диагоналей прямоугольника до его смежных сторон равно 3,2 см и 3,2 см. начерти рисунок и вычисли периметр прямоугольника....
ЕваЛя ЕваЛя  29.06.2019 04:40
Решите : два катета прямоугольного треугольника равны 5 и 12. найдите его площадь....
tsts84 tsts84  15.11.2020 15:50
Дано вектори р= (1; -5) i q= (3; 1). Знайдіть скалярний добуток век- торів: а решите​...
0987123456530 0987123456530  15.11.2020 15:51
решите и оформите на листке умоляю ❤️❤️❤️...
odimaa1dimas odimaa1dimas  15.11.2020 15:51
Основи трапеції дорівнюють 18 см і 6 см. Середня лінія поділяється діагоналями на три частини. Знайдіть їхні довжини...
destroyer0800 destroyer0800  15.11.2020 15:51
Используя рисунок , укажите прямую, скрещивающуюся с прямой АВ и принадлежащую плоскости АВВ1....
kajaiuw kajaiuw  16.10.2019 17:29
Висота правильної чотирикутної призами 5см а сторона основи 4см а)знайти площю поверхні б)довжину її діагоналі...
maksim20081986 maksim20081986  16.10.2019 17:29
1.угол между диагоналями прямоугольника равен 80°.найдите углы между диагональю прямоугольника и его сторонами. 2.в ромбе авсd диагонали пересекаются в точке о, 3.в прямоугольнике...
плаг плаг  16.10.2019 17:29
Втрапеции abcd угол а =60 градусов, угол d =45 градусов, боковые стороны равны 10 и 12 см, а меньшее основание 8 см, найдите среднюю линию трапеции...

Популярные вопросы