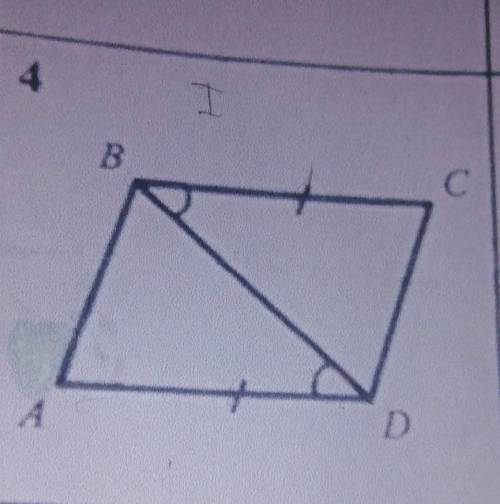
Найти пары равных треугольников и доказать их равенство:​

DBC=BAD

Объяснение:

BD-общая

DAC=BDA

AD=BC

Для того чтобы найти и доказать равенство пар треугольников, мы должны сравнить их стороны и углы. Давайте рассмотрим каждую пару треугольников поочередно.

1) Рассмотрим треугольник ABC и треугольник DEF. По условию, мы знаем, что стороны треугольников равны правильно:

AB = DE = 4 см

AC = DF = 6 см

BC = EF = 5 см

Также, у нас есть информация о том, что угол BAC равен углу EDF.

Для доказательства равенства треугольников ABC и DEF, мы можем использовать один из следующих критериев равенства треугольников.

- Критерий равенства по двум сторонам и углу между ними (ССА).

Так как мы знаем, что стороны AB и DE равны, стороны AC и DF равны, и угол BAC равен углу EDF, мы можем применить данный критерий. ССА критерий утверждает, что если две стороны и угол, заключенный между ними, треугольника равны соответственно другим двум сторонам и углу другого треугольника, то эти треугольники равны.

Таким образом, треугольники ABC и DEF равны.

2) Рассмотрим треугольник PQR и треугольник XYZ. По условию, мы знаем, что стороны треугольников равны правильно:

PQ = XY = 5 см

PR = XZ = 7 см

QR = YZ = 6 см

Также, у нас есть информация о том, что угол PQR равен углу XYZ.

Мы можем использовать аналогичный критерий ССА для доказательства равенства треугольников PQR и XYZ.

Таким образом, треугольники PQR и XYZ равны.

Таким образом, мы нашли две пары равных треугольников и доказали их равенство, используя критерий равенства по двум сторонам и углу между ними.

Надеюсь, эта подробная информация помогла вам понять решение задачи! Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать их.