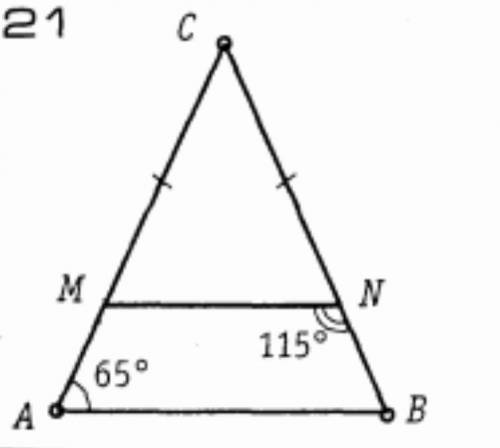
Найти параллельные прямые и доказать их параллельность
Другие вопросы по теме Геометрия
Популярные вопросы
- 4тонны сколько кубических метров...
3 - 40 ! задайте с перечисления элементов множество: 1) а={х | х є z,...
3 - Вес человека, стоящего на полу, 700 н. с какой силой пол действует...
3 - Дано треугольник abc прямоугольный,угол c=90 градусов,cm медиана,...
3 - Выражение : 128x^2 y^3 *(-1/4xy^5)^3 для тех кто не понял - 128х...
2 - Плоха та птица, которой родное гнездо не мило безударная гласная...
1 - Вставь в пустые клетки такие цифры , чтобы при округлении делимого...
1 - Играем с друзьями — придумайте другое название, на эту же тему....
1 - Вопросыопределение «биоценоз,? . какие три компонента составляют...
1 - 1.найти номер минимального элемента массива. 2. найти номера минимального...
2
угол N = углу А - как внутренние односторонние
Угол N = 115°
Угол А = 65°
115°+65° = 180°
Следовательно, прямые параллельны по третьей теореме параллельности прямых (Если сумма внутренние односторонних углов равна 180° градусов, то прямые параллельны)
MN и АВ
Объяснение:
1) Найдём угол <МNC
<MNC = 180° - <MNB = 180° - 115° = 65°
2) Рассмотрим треугольник МСN
Он равнобедренный (MC = CN), а значит, согласно его свойствам, углы при основании равны, то есть
<CMN = <MNC = 65°
3) Если при пересечении двух прямых секущей выполняется хотя бы одно из условий:
- внутренние разносторонние углы равны;
- сумма внутренних односторонних углов равна 180°;
- соответствующие углы равны;
• Мы видим две прямые MN и АВ, и их секущую АС. При этих прямых и этой секущей соответсвующие углы (<CMN и <САВ) равны, а значит сами прямые параллельны •