1. Геометрия
  2. Найти объём правильной треугольной

Найти объём правильной треугольной призмы, все ребра которой равны 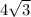4\sqrt{3}

klybnika228 klybnika228    3   09.12.2021 21:22    459

Ответы
kamilachelny kamilachelny  11.01.2024 10:06
Чтобы найти объем треугольной призмы, нужно умножить площадь основания на высоту.

Для начала, найдем площадь основания призмы. Основание треугольной призмы - это равносторонний треугольник. У нас дана сторона равна 4\sqrt{3}, поэтому мы можем легко найти площадь треугольника.

Формула площади равностороннего треугольника:
S = (a^2 * √3) / 4

Где a - длина стороны треугольника.
Подставляя значение стороны, получаем:
S = (4√3^2 * √3) / 4 = (4 * 3 * √3) / 4 = 3√3.

Теперь, чтобы найти объем призмы, нужно умножить площадь основания на высоту.
В данном случае, все ребра призмы равны 4\sqrt{3}, поэтому высота призмы также будет равна 4\sqrt{3}.

V = S * h
V = 3√3 * 4√3 = 12 * √3 * √3 = 12 * 3 = 36.

Ответ:
Объем правильной треугольной призмы, все ребра которой равны 4\sqrt{3}, равен 36.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
WhiteRos WhiteRos  14.05.2020 10:47
Как у и по Тито не хочу тебя увидеть не только в понедельник в первой необходимости в принтере или подключении к интернету для регистрации на сайте и...
tsybizovaanya tsybizovaanya  14.05.2020 10:47
1. Составьте общее уравнение прямой проходящей через точки А(0; 3) и В(-1;0) 2. Точки О(0;0), А(12; 8), C(4; 6) и B являются вершинами параллелограмма. Найдите абсциссу...
Тупой7А Тупой7А  14.05.2020 10:47
Пряма МК паралельна стороні АС трикутника АВС. Кут 1 = 60 градусів, а кут 2 = 72 градуси. Знайдіть кути А і С трикутника решите...
ksish456 ksish456  14.05.2020 10:30
ответы к семестровой контрольной по геометрии...
monkeyone monkeyone  14.05.2020 10:47
ABCDA1B1C1D1 — куб с ребром, равным4 см.а) Постройте сечение кубаплоскостью, проходящей через точкиK, C и D1, где K — середина ребра AB.б) Вычислите периметр P сечения....
Macsum204 Macsum204  14.05.2020 10:47
При перетині двох прямих, один із кутів, що утворився дорівнює 35 градусів. Скільки градусів дорівнює кут між прямими...
vanyalebedev1248 vanyalebedev1248  14.05.2020 10:47
На единичный окружности с центром в начале координат изобразите точку,полученную поворотом точки А0(1;0) на угол: А)3П Б)5П/2 В)-3П/4 Г)-7П Я ГУМАНИТАРНЫЙ ЧЕЛОВЕК ДАМ 10+...
obuhovasveta obuhovasveta  14.05.2020 10:47
Визначте рядок, у якому лише сполучники.А) чи, щоб, як, для того щоб, крізь. Б) понад, якщо, як тільки, та.В) аби, ніби, проте, дарма що. Г) зате, немов, хоч…хоч, поблизу.2.Визначте...
антон776 антон776  14.05.2020 10:47
Один з, кутів що утворився при перетині двох паралельних прямих січною, дорівнює 78 градусів. Знайти градусні міри решти 7 кутів?...
аленкатв3 аленкатв3  14.05.2020 10:47
Точка М делит отрезок РК на две равные части. Найдите координаты точки Р, если точки М и К имеют соответственно координаты (3;-5), (4; 6). 2. а) Изобразите окружность,...

Популярные вопросы