Найти экстремумы функции. Геометрия
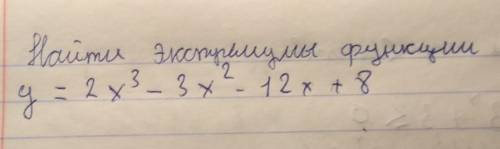
Другие вопросы по теме Геометрия
Популярные вопросы
- НАГРАДА написать что такое: • Размножение • Раковинные амебы, радиолярии,...
1 - Внешняя и внутренняя политика Марии Кровавой...
3 - Розкажіть, що ви знаєте про С. Фіоля, Фр. Скорину й І. Федорова...
1 - Я купил компьютер 2-3 месяца назад(сам собирал). И где то через...
3 - Выражение, записанное на картинке, читается как 105+92, то есть...
1 - Тематичний контроль з біології (за ответ не по теме - бан) ...
1 - Сколько квадратных метров равна площадь двора?...
2 - Добрати приклад до кожного випадку ...
1 - Чому диференційовані зуби з явились лише у ссавців?...
1 - II.Составьте предложения из слов с переводом. 1. family, New Year,...
2
x₁=2; y= -12 min
x₂= -1; y= 15 max
Объяснение:
y(2)=16-12-24+8= -12;
y( -1)= -2-3+12+8= 15
Відповідь:
Пояснення:
Перша прохідна функції:
y' = 6·x^2-6·x-12
6·x^2-6·x-12 = 0
x1 = -1
x2 = 2
__+-1-2+>y'
зростає max спадає min зростає
Обчислимо значення функції
f(-1) = 15
f(2) = -12
Відповідь:
fmin = -12, fmax = 15