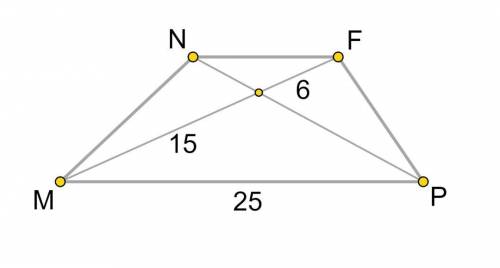
Найти длину меньшего основания трапеции, изображенной на рисунке.

Чтобы найти длину меньшего основания трапеции, изображенной на рисунке, нужно использовать знание о свойствах трапеции.

Трапеция - это четырехугольник с двумя параллельными сторонами, которые называются основаниями. Зная, что сторона AD параллельна стороне BC, мы можем сделать вывод о том, что сторона AC является диагональю трапеции.

Обозначим длину меньшего основания трапеции как x. Тогда длина большего основания будет равна 2x, так как говорится, что она в два раза длиннее меньшего основания.

Заметим также, что диагональ AC разбивает трапецию на два треугольника: ABC и ACD.

Так как сторона BC и сторона AD параллельны, треугольники ABC и ACD являются подобными треугольниками. Это значит, что их соответствующие стороны пропорциональны.

Мы можем построить пропорцию между сторонами треугольников ABC и ACD, используя соответствующие стороны:

BC/AC = AC/CD

Так как мы знаем, что сторона BC равна 2x и длина диагонали AC равна 6 см (это можно определить, измерив на рисунке), мы можем подставить эти значения в пропорцию:

2x / 6 = 6 / CD

Теперь мы можем решить эту пропорцию, чтобы найти длину CD:

2x * CD = 6 * 6

2x * CD = 36

CD = 36 / 2x

CD = 18 / x

Таким образом, мы получаем, что длина диагонали CD равна 18 / x.

Согласно свойствам трапеции, диагональ CD делит большее основание пополам. Значит, CD равна половине длины большего основания.

Мы знаем, что большее основание равно 2x, поэтому:

18 / x = 2x / 2

18 / x = x

Теперь мы можем решить это уравнение:

x^2 = 18

x = sqrt(18)

x примерно равно 4.24

Таким образом, длина меньшего основания теперь известна - она примерно равна 4.24 см.