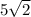Найти диагональ куба, если боковая поверхность куба равна 100см^2
Другие вопросы по теме Геометрия
Популярные вопросы
- Узнай когда и как образуются овраги...
1 - Увеличьте число а на р%, уменьшите число а на р%, если: а=40, р=10 а=50,р=50...
2 - Нужна презентация (на )про любого поэта ()...
1 - Вколлекции юры 750 марок в трех больших альбомах по 150 марок а в нескольких по...
1 - Напиши текст из ключевых слов : народный праздник и катание на санках...
3 - №1 найти область определения и значения функции. а) y=cos x/3 - 1 б) y=sin 3x...
2 - Написать сочинение на тему подлость...
3 - 10 слов с орфограммой проверяемые согласные в корне слова...
3 - За 1 час убрали картофель 3 картофеляуборочных комбайнамогут с поля площадью 12...
1 - Слово повстречался орфографический разбор.зарание )...
2
Відповідь:
Пояснення:
Для начала найдем площадь одной стороны куба. Для этого поделим боковую площадь на 6(так как сторон в сумме 6), имеем: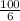 =
= 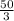
Площадь одной стороны равна квадрату длины куба, отсюда имеем: а =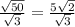
Далее найдем Диагональ стороны, по т. Пифагора: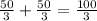
Извлекаем корень: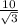
И последний шаг, опять теорема Пифагора, только уже для стороны и диагонали стороны: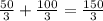
Извлекаем корень и упрощаем: