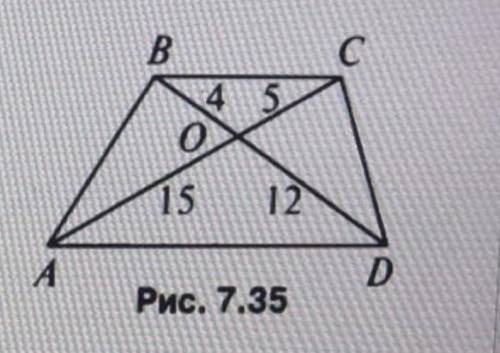
Найти: BC
BO=4
OC=5
OD=12
AO=15

Объяснение:

АО/СО=DO/BO

15/5=12/4=3 - стороны пропорциональны , <AOD=<COB - как вертикальные, значит тр-к АОD ~ тр-ку СОВ по двум пропорциональным сторонам и углу между ними

Коэффициент подобия к=3

АD/BC=3

BC=AD/3

ответ : ВС=АD/3

Для решения данной задачи нам понадобятся основные свойства геометрических фигур и теоремы.

Из предоставленного изображения видно, что мы имеем дело с прямоугольным треугольником AOC, где прямой угол находится в точке O. Также известны значения некоторых сторон: BO=4, OC=5, OD=12 и AO=15. Мы должны найти значение стороны BC.

Для начала, давайте вспомним основные свойства прямоугольного треугольника.
1) В прямоугольном треугольнике гипотенуза всегда является наибольшей стороной, которая противоположна прямому углу. В нашем случае это сторона AO.
2) Теорема Пифагора: в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Мы можем использовать эту теорему, чтобы найти длину стороны BC.

Теперь, рассмотрим наше изображение.

Из предоставленных данных мы видим, что AO=15. Для решения задачи нам необходимо найти сторону BC. Мы знаем, что AO является гипотенузой прямоугольного треугольника AOC, а OC является одним из катетов. Следовательно, мы можем использовать теорему Пифагора для нахождения BC.

Сформулируем использованную нами теорему Пифагора: в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Теперь, заменим известные значения в данную формулу:

OC^2 + BC^2 = AO^2

Подставим известные значения:

5^2 + BC^2 = 15^2

Решим данный квадратный уравнение:

25 + BC^2 = 225

BC^2 = 225 - 25

BC^2 = 200

Теперь, возьмем квадратный корень от обеих частей уравнения:

BC = sqrt(200)

Осталось упростить полученное значение:

BC = sqrt(2 * 2 * 2 * 5 * 5)

Так как 2 и 5 являются простыми числами, мы можем записать корень из них отдельно:

BC = 2 * 5 * sqrt(2)

Следовательно, длина стороны BC равна 10 * sqrt(2).

Таким образом, ответ на задачу: BC = 10 * sqrt(2).