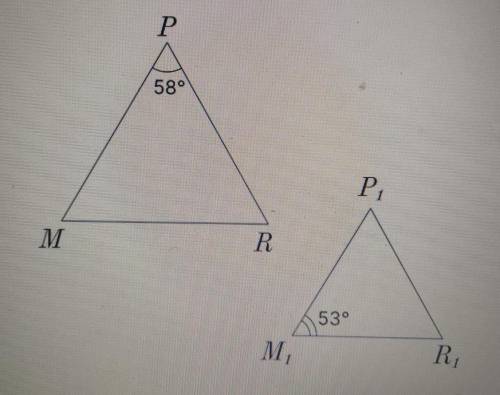
Найдите значение угла r и r1

В задании не сказано-подобны ли Треугольники?

Если подобны,то

<Р1=<Р=58 градусов

<М1<М=53 градуса

<R=<R1=180-(58+53)=180-111=69 градусов

Объяснение:

Для того чтобы найти значение угла r и r1, нам понадобятся некоторые свойства треугольника и его внутренних углов.

1. Заметим, что в треугольнике ABF со сторонами AB, AF и BF мы можем применить теорему косинусов:
AF^2 = AB^2 + BF^2 - 2 * AB * BF * cos(r)

Используя данное выражение, можно выразить BF через AF и AB:
BF = (AF^2 + AB^2 - AF^2 * cos(r)) / (2 * AB)

2. Также мы можем использовать теорему синусов для треугольника ABF:
AB / sin(r) = AF / sin(60°) (1)

Аналогичным образом, для треугольника BCF:
BC / sin(r1) = BF / sin(60°) (2)

Обратим внимание, что AB = BC, так как это боковая сторона правильного шестиугольника.

3. Если мы возьмем соотношение (1) и разделим его на (2), получим выражение, содержащее только углы r и r1:
(AB / sin(r)) / (BC / sin(r1)) = (AB / BF) = (sin(60°) / sin(60°))

Из последнего равенства мы можем выразить BF через углы r и r1:
BF = AB * (sin(r) / sin(r1))

Зная это, мы можем подставить выражение для BF в уравнение из пункта 1:
(AF^2 + AB^2 - AF^2 * cos(r)) / (2 * AB) = AB * (sin(r) / sin(r1))

Сокращаем AB с обоих сторон:
(AF^2 + AB^2 - AF^2 * cos(r)) / 2 = AB^2 * (sin(r) / sin(r1))

Раскрываем скобки:
AF^2 + AB^2 - AF^2 * cos(r) = 2 * AB^2 * (sin(r) / sin(r1))

Далее приведем подобные слагаемые:
AB^2 - AF^2 * cos(r) = AB^2 * (sin(r) / sin(r1))

Получаем окончательное выражение для нахождения угла r:
cos(r) = (AB^2 - AB^2 * (sin(r) / sin(r1))) / AF^2

Для решения этого уравнения, можно применить методы решения квадратных уравнений или использовать табличные или программные средства для вычисления значения.

4. Теперь найдем значение угла r1. В треугольнике BCF, мы можем использовать теорему синусов:
BC / sin(r1) = BF / sin(60°)

Подставляем выражение для BF, полученное ранее:
BC / sin(r1) = AB * (sin(r) / sin(r1)) / sin(60°)

Сокращаем sin(r1) с обоих сторон:
BC = AB * (sin(r) / sin(60°))

Делаем замену AB = BC (так как это боковая сторона правильного шестиугольника):
BC = BC * (sin(r) / sin(60°))

Получаем окончательное выражение для нахождения угла r1:
sin(60°) = sin(r)

В этом случае, значение угла r1 уже известно и равно 60°.

Таким образом, чтобы найти значение угла r, мы должны решить квадратное уравнение, а угол r1 равен 60°.