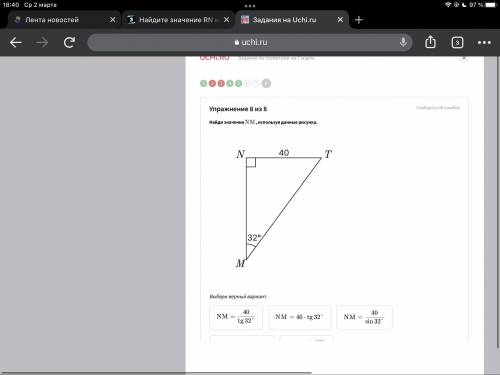
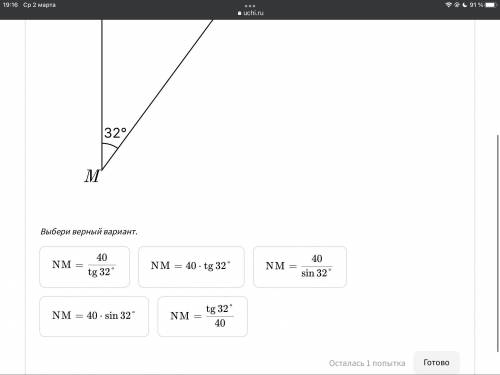
Найдите значение MN используя данные рисунка

Для решения данного вопроса, мы должны использовать информацию, представленную на рисунке.

Давайте рассмотрим первый рисунок. На нем изображена прямая AB, которая пересекает прямую CD. Заметим, что эти две прямые являются параллельными, потому что они имеют одинаковое направление и не пересекаются. Теперь мы знаем, что при параллельных прямых, соответствующие углы равны. Это значит, что угол DMN равен углу BAC.

На втором рисунке, видно, что угол BAC равен 57 градусов. Следовательно, угол DMN также равен 57 градусов.

Дальше, заметим, что угол DMN является внутренним углом треугольника DMN, а значение этого угла равно 57 градусов. Поскольку в треугольнике сумма всех внутренних углов равна 180 градусов, мы можем записать уравнение:

Угол DMN + Угол NDM + Угол MND = 180 градусов.

Заметим, что угол NDM и угол MND являются вертикальными углами, поскольку они соответствующие углы по отношению к пересекающимся прямым DM и CD. Вертикальные углы равны. Поэтому угол NDM равен 57 градусов, а угол MND также равен 57 градусам.

Подставим значения углов в уравнение:

57 градусов + 57 градусов + Угол MND = 180 градусов.

Сложим первые два угла:

114 градусов + Угол MND = 180 градусов.

Теперь вычтем 114 градусов из обеих сторон уравнения:

Угол MND = 180 градусов - 114 градусов.

Угол MND = 66 градусов.

Таким образом, мы нашли значение угла MND, которое составляет 66 градусов.

Но нам необходимо найти значение длины MN. Обратим внимание, что угол MND является прямым углом, поскольку это угол между прямыми MN и CD. Прямой угол равен 90 градусам.

Теперь у нас есть два угла треугольника DMN: угол MND = 66 градусов и прямой угол = 90 градусов. Известно, что сумма углов треугольника равна 180 градусам.

Подставим значения углов в уравнение:

66 градусов + 90 градусов + Угол MDN = 180 градусов.

Сложим первые два угла:

156 градусов + Угол MDN = 180 градусов.

Теперь вычтем 156 градусов из обеих сторон уравнения:

Угол MDN = 180 градусов - 156 градусов.

Угол MDN = 24 градуса.

Теперь, у нас есть два угла треугольника DMN: угол MND = 66 градусов и угол MDN = 24 градуса. Сумма всех углов треугольника равна 180 градусов.

Подставим значения углов в уравнение:

24 градуса + 66 градусов + Угол NDM = 180 градусов.

Сложим первые два угла:

90 градусов + Угол NDM = 180 градусов.

Теперь вычтем 90 градусов из обеих сторон уравнения:

Угол NDM = 180 градусов - 90 градусов.

Угол NDM = 90 градусов.

Теперь мы знаем, что угол NDM равен 90 градусов. Заметим, что угол NDM является прямым углом, поскольку это угол между прямыми MN и DM. Прямой угол равен 90 градусам.

Таким образом, мы можем заключить, что угол NDM является прямым углом и его значение равно 90 градусам. Значит, угол NDM является прямым углом.

Теперь мы получили прямоугольный треугольник в треугольнике DMN с углом NDM = 90 градусов. Нам нужно найти длину стороны MN.

Мы знаем, что в прямоугольных треугольниках длина стороны, которая является гипотенузой, связана с длинами двух других сторон по теореме Пифагора:

a^2 + b^2 = c^2,

где a и b - длины катетов, а c - длина гипотенузы.

В нашем случае, сторона MN является гипотенузой, а стороны DM и DN - катетами.

Подставим значения в формулу:

DM^2 + DN^2 = MN^2.

Заметим, что отрезок DM имеет длину 14, а отрезок DN имеет длину 48.

Подставим значения:

14^2 + 48^2 = MN^2.

Выполним необходимые вычисления:

196 + 2304 = MN^2.

2500 = MN^2.

Чтобы найти значение MN, возьмем квадратный корень от обеих сторон:

MN = √2500.

Мы знаем, что 50 * 50 = 2500, поэтому:

MN = 50.

Таким образом, мы нашли значение MN, которое равно 50.