Найдите высоту ромба со стороной 10 см и диагональю 12 см.

Ромб является частным случаем параллелограмма, значит его площадь как параллелограмма равна: S=ah, где a - сторона ромба, h - его высота.

С другой стороны, площадь ромба равна половине произведения его диагоналей.

Диагонали ромба перпендикулярны и пересекаются в точке, делящей их пополам.

Значит образуется прямоугольный треугольник. В нашем случае с гипотенузой 10 и катетом 6

Тогда половина второй диагонали ромба равна: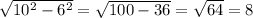

Значит вторая диагональ равна 8*2=16

S=(16*12)/2=96

h=S/a=96/10=9,6

По формуле: S=ah, где a-сторона ромба, h-высота.

По рисунку видно,что половина диагонали равна 6 см.

Тогда половина второй диагонали ромба равна: см

Значит вторая диагональ равна 8*2=16см

S=(16*12)/2=96см

Значит h=S/a=96/10=9,6см

ответ:9,6см