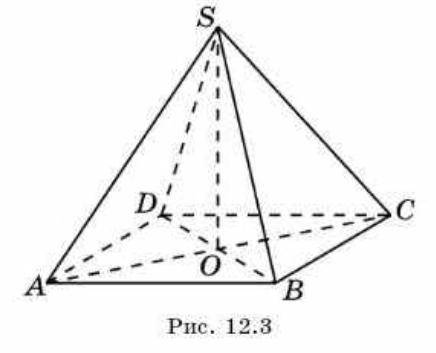
Найдите высоту правильной четырехугольной пирамиды SABCD все ребра которой равны 1

Так как по условию задачи пирамида правильная, то в основании – квадрат. Диагональ квадрата равна произведению его стороны на √2, то есть d = √2·а

а = AB=BC=CD=AD = 1 (ед.измер.) по условию задачи

d = АС = BD = √2 · 1 = √2

Половина диагонали АО = AS/2 = √2/2

По условию задачи все рёбра пирамиды равны, поэтому SA = SB = SC = SD = 1 (ед.измер.) Из прямоугольного ΔAOS:

SO = √АS² -  АО² = √1² - (√2/2)² = √2/2

ответ:  √2/2 (ед.измер.)