Найдите все неизвестные углы треугольника надо прямо сейчас
Другие вопросы по теме Геометрия
Популярные вопросы
- Найти словосочетания в предложении с листьев дождинки скатываются на...
1 - Составить рисунки к (решение необязательно): №1: один из внешних углов...
2 - Решить расставьте знаки препинания в тексте. по внешности сестры до...
1 - Дано abcd - прямоугольник , p abcd = 44 ,dc : ad = 7 : 4 , найти s...
2 - Составьте предложения на и 1 hove/ you/ book/ that/ read/ yet/ travel?...
3 - А)найди на карте и перечисли пустыни тропического климатического пояса...
2 - Петрик зловив 6 рибин і ще дві третини улову. скільки рибин спіймав...
3 - Решите : из двух пунктов, расстояние между которыми равно 89 км, одновременно...
3 - Як встановити закономірність і продовжити числовий ряд 28см+19см= см...
2 - Характеристика хлора и аммиака. предмет-(обж) ! ....
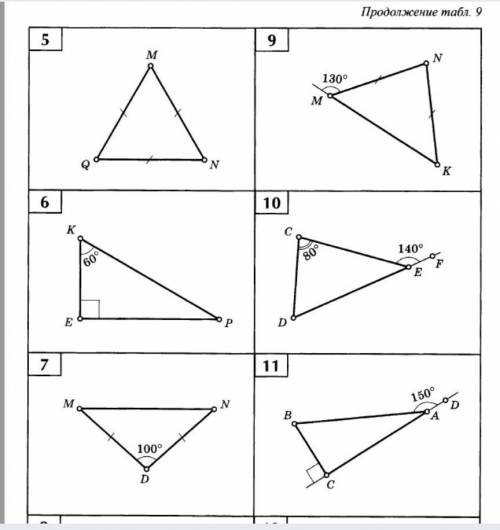
3
5) ∠Q=∠M=∠N=180°:3=60° все стороны равны- Δ равносторонний и у него все углы равны по теореме о сумме трёх углов Δ
∠Q=∠M=∠N=180°:3=60°
6)∠E=90°;
∠P=90°-60°=30° по теореме о сумме острых углов прямоугольногоΔ.
7) MD=DN, ΔMDN- равносторонний,∠M и∠N- углы при основанииΔ
∠M=∠N=(180°-100°)/2=40°.
9) MN=NK, ΔMNK - равносторонний ∠M и∠K - углы при основанииΔ
∠M=180°-130°=50°; как смежный с внешним∠
∠M=∠K=50°;∠N=130°-∠K=80°.( как сумма двух углов против внешнего угла треугольника)
10)∠E=180°-140°=40°; как смежный с ∠CEF
∠D=180°-80°-40°=60° ( по теореме о сумме трёх углов).
11)∠C=90, ∠A=180°-150°=30°; ∠B=90-30°=60° по теореме о сумме острых углов прямоугольногоΔ.
5) Все углы 60° (равносторонний треугольник)
6) ∠KPE=90-60=30°
7) ∠PMN=∠MNP=(180-100)\2 = 40°
9) ∠NMK=∠NKM=180-130=50°
∠MNK=180-100=80°
10) ∠CED=180-140=40°
∠CDE=180-(80+40)=60°
11)∠BAC=180-150=30°
∠CBA=90-30=60°