Найдите величину угла САВ, если сумма всех углов  треугольника равна 180° ( на конце C)

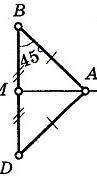
Чтобы найти величину угла САВ, нам нужно использовать свойство треугольника, согласно которому сумма всех углов в треугольнике равна 180°. 1. Давайте обратимся к изображению треугольника ABC. Вам нужно найти угол САВ, это угол, расположенный напротив стороны BC. 2. Здесь мы можем использовать свойство парных углов при пересечении двух прямых линий, называемое также свойством вертикальных углов. 3. Вертикальные углы - это пары углов, которые находятся напротив друг друга, когда две прямые линии пересекаются. В нашем случае угол В и угол САВ являются вертикальными углами. 4. По свойству вертикальных углов, мы знаем, что вертикальные углы равны. То есть меры угла В равна мере угла САВ. 5. Итак, чтобы найти меру угла САВ, нам нужно найти меру угла В. 6. Обратимся к другим данным в диаграмме. Мы знаем, что мера угла А равна 80°, а мера угла ВАС равна 50°. 7. Теперь мы можем найти меру угла В путем вычитания углов А и ВАС из суммы углов треугольника АВС. 8. Сумма углов треугольника равна 180°, значит, мы можем записать уравнение: А + В + С = 180°. 9. Подставим известные значения в уравнение: 80° + В + 50° = 180°. 10. Складываем известные значения: 130° + В = 180°. 11. Теперь вычтем 130° из обеих сторон уравнения: В = 180° - 130°. 12. Вычисляем: В = 50°. 13. Мы нашли меру угла В равной 50°. 14. Используя свойство вертикальных углов, мы знаем, что угол САВ равен мере угла В. 15. Ответ: величина угла САВ равна 50°.