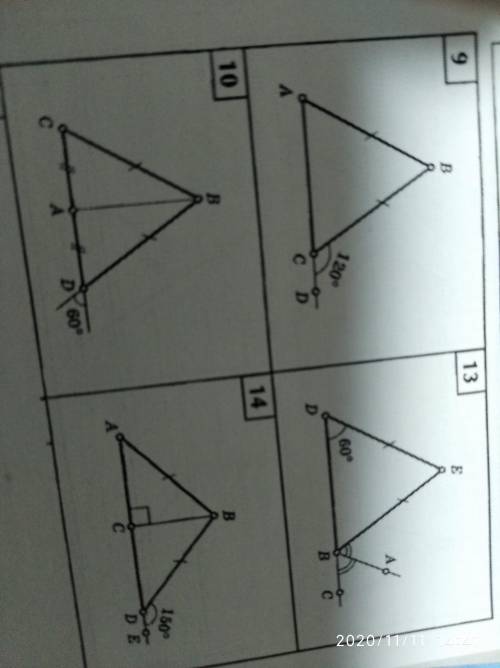
Найдите угол СВА на всех рисунках
Другие вопросы по теме Геометрия
Популярные вопросы
- Розв язати задачу і масою 200г з масовою часткою натрій хлориду...
3 - Н до рівняння.Конструктивно Ейфелева вежа складається зтрьох частин....
3 - Проблема не стандартная! Хотел переустановить игру. Удалил, вылетела...
2 - Построить треугольник по стороне и двум прилежащим к ней углам....
1 - Сколько натуральных решений неравенства 3с -2,7 принадлежит промежутку...
2 - Решите физику Номер 12 13 14 ...
1 - 3. Тірек сөздерді пайдалана отырып, тілек жазыңдар.Жүлдызы жарқырау;...
3 - 7. Подбери по 3 имени прилагательных к именам существительным,...
1 - Решите хотя бы что то пожплуйста. буду благодарен)...
1 - №1. В прямоугольном ΔАВС ∠С= 90°, АВ=10 см, ВС=5 см. Найдите углы,...
2
- Рассмотрим первый рисунок.
Мы видим треугольник СВА. У нас нет никакой информации о величине других углов треугольника, поэтому предположим, что все углы равны. Пусть каждый угол будет обозначаться буквой "х". Тогда мы можем записать уравнение:
х + х + х = 180
3х = 180
Теперь мы можем найти значение угла "х", разделив обе стороны уравнения на 3:
х = 180 / 3
х = 60
Таким образом, угол СВА в этом треугольнике равен 60 градусам.
- Рассмотрим второй рисунок.
Здесь у нас также нет информации о других углах треугольника. Примем, что все углы треугольника равны и обозначим их буквой "у". Запишем уравнение:
у + у + у = 180
3у = 180
Разделим обе стороны на 3:
у = 180 / 3
у = 60
Таким образом, угол СВА во втором рисунке также равен 60 градусам.
Вывод: Угол СВА равен 60 градусам на обоих рисунках.