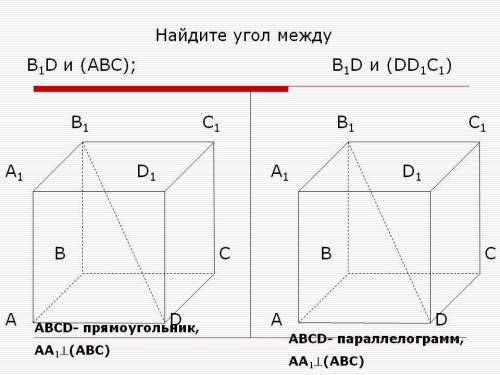
Найдите угол между В1D и (ABC); В1D и (DD1C1)

Найдите угол между В1D и (ABC); В1D и (DD1C1)

Объяснение:

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость ( в качестве угла между прямой и плоскостью  выбирается острый угол ).

Для нахождения угла между линиями В1D и (ABC), мы должны использовать знания о геометрических свойствах углов и свойствах параллельных линий. Давайте разберемся с каждым шагом в отдельности.

Шаг 1: Определение параллельных линий
Мы видим, что линии (ABC) и (DD1C1) параллельны друг другу. Это означает, что уголы, образованные этими линиями со В1D, будут соответствующими углами.

Шаг 2: Нахождение B1D угла с линией (ABC)
По определению соответствующих углов, угол между линией В1D и (ABC) будет равен углу АВ1D.

Шаг 3: Нахождение АВ1D угла
Мы знаем, что АВ и В1С являются противоположными углами, так как они лежат на пересекающихся прямых линиях AB и B1C1. Поэтому, АВ1D угол будет равен В1C углу.

Шаг 4: Нахождение угла В1C
Так как линии B1С1 и ВС параллельны (по условию), то они будут образовывать соответствующие углы. Значит, угол В1C будет равен АВ углу.

Шаг 5: Нахождение угла АВ
Мы видим, что ВВ1C1 и ABC - вертикальные углы, поэтому угол АВ будет равен углу В1C1.

Шаг 6: Нахождение угла В1C1
Мы знаем, что уголы В1C1 и DD1C1 являются вертикальными углами, так как они лежат на пересекающихся прямых линиях B1C1 и DC1. Поэтому, угол B1C1 будет равен DD1C.

Таким образом, чтобы найти угол между линией В1D и (ABC), мы должны рассмотреть следующую последовательность углов: АВ1D, В1C, АВ, В1C1 и DD1C1.

В конечном итоге, чтобы найти угол между линией В1D и (ABC), мы должны найти угол DD1C. Для этого вам нужно знать значения всех других углов (АВ1D, В1C, АВ, В1C1 и DD1C1) и использовать соответствующие обозначения на вашей диаграмме, чтобы найти нужный угол.

Однако, с учетом только предоставленной диаграммы, невозможно точно определить значения всех этих углов. Для полного решения данной задачи необходимы дополнительные данные или углы.