Найдите угол между касательной и хордой, которые проведены из одной точки, если хорда равна половине диаметра окружности.

Очевидно, этот угол равен 30 градусам. Длина хорды равна радиусу. Треугольник с вершинами : центр окружности , концы хорды -равносторонний. Одна из его сторон перпендикулярна касательной. Отсюда ответ: 90-60=30.

Пользуясь рисунком, (см. вложение) и зная, что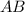 — диаметр окружности, 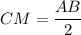— хорда окружности, определим .

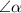В окружности половиной диаметра являются радиусы, значит, эти радиусы будут равны и хорде: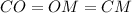

В образовавшемся треугольнике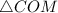 получается, что все три стороны по длине равны, следовательно, этот треугольник является равносторонним, у которого все углы равны по .

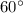Как известно, точка касания касательной к окружности и радиуса окружности пересекаются под прямым углом ().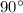

Отсюда следует, чтобы узнать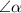 , нужно найти разность развёрнутого угла (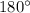) от суммы других известных углов:

ответ: 30°