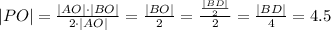Найдите радиус окружности , вписанный в ромб, большая диагональ которого равна 18см, а тупой угол ромба равен 120гр.
Другие вопросы по теме Геометрия
Популярные вопросы
- По горизонтальной стальной поверхности равномерно тянут изготовленное из...
1 - С20 девочек играли с 19 мальчиками 11 девочек ушли а 16 мальчиков ушло сколько...
2 - Вавтосалоне за неделю подарили 37 легковых машин и на 7 меньше грузовых.сколько...
1 - Агрегатное состояние вещества напишите применение каждому: газообразные жидкие...
3 - Найти грамматическую основу и начертить схему двух этих предложений шли они...
2 - Написать небольшой текст-рассуждение по пословице за морем веселье, да чужое,...
3 - Скакой сила тело объёма 1 дм 3 кубическихсантиметра будет выталкиватся из...
1 - Вера сделала 6 загладок для книг. она подарила брату 2загладки...
1 - Қыста торғайлар ұясына мамық таси бастаса,күн қатты суытады сөйлем мүшелері...
1 - Замените слова : постепенно,не так как раньше, новым по новому наречиями...
3
Пусть ромб - ABCD. O - точка пересечения диагоналей. OP - перпендикуляр из точки О на AB. Диагонали ромба пересекаются под прямым углом.
Рассмотрим прямоугольные треугольники PBO и OBA. Они подобны по 2-м углам.
Таким образом: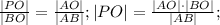
угол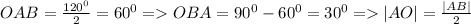
Т.о.