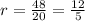Найдите радиус окружности, вписанной в ромб с диагоналями 6 см и 8 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- ответьте на вопросы: 1) do you find language learning difficult? 2) what do...
2 - Охарактеризуйте роль международных группировок в мировом хозяйстве....
1 - Складіть опис одного з героїв з твору п ятнадцятирічний капітан...
2 - Написать рекламу про компьтер,телефон и так далее...
3 - :из множества чистых цветков лотоса были принесены в жертву; шиве - третья...
1 - Какой объем 4,9 % -ного р-ра h2so4 плотностью 1,03 г / мл потребуется для растворения...
2 - Выберу самое лучшее решение.сообщение о питание жителей древней руси....
1 - Tom has got a frog.the frog got big.it точек нужно вставить слова?...
1 - Запишите уравнение реакции разложение нитрата серебра, если в результате нее...
1 - Скороссворд в ! мореплаватель! 7 букв...
1
Заметим, что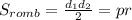 , где p-полупериметр ромба.
, где p-полупериметр ромба.
Так как в ромбе диагонали пересекаются под прямым углом и точкой пересечения делятся пополам, то у нас образуется прямоугольный треугольник с катетами 3 и 4 см. Тогда гипотенуза этого прямоугольного треугольника равна 5см (по теореме Пифагора), и эта гипотенуза равна стороне ромба. Значит, полупериметр ромба равен 5*4/2=10 см.
Приравняем формулы площади ромба (см. выше), получим:
Найдём r: